Newみんなの算数講座44 数表シリーズ①三角数

こんにちは。今日も読みにきてくれてありがとうございます。
今回の講座44は、改訂しているニューみん算で4作目になる新作です。できるだけ元祖の講座を活かして読みやすく改訂したいのですが、元祖には問題だけ出していた回もあったんですね。ニューみん算ではその企画はやらないことにしたので旧44番は新作に差し替えました。
新作のテーマは44講座目で初となる数表です。与えられた数表の一部から規則性を見抜き、その規則性を大いに活用して設問に答えるタイプの問題ですね。もちろん設問で聞かれるのは与えられた数表にはのっていない部分だから、数表全体で変わらない規則を的確につかんで対処することが大事です。一つの規則だけでは不安なので、二つか三つの規則が見抜ければ十分戦えますね。では問題を出して解説するいつものパターンで進めましょう。
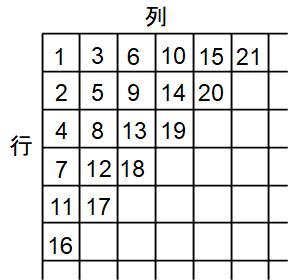
下の表のように整数を規則正しく並べていきます。この数表のタテを行、横を列と呼ぶことにします。たとえば3行4列の数は19です。次の各問いに答えてください。
(1)7行5列の数はいくつですか?
(2)12行18列の数はいくつですか?
(3)777は何行何列にありますか?
これと同じ数表はとてもよく出題されます。いくつか特長があるので、まずその特長を整理してみます。下の図を見ながら確認してください。
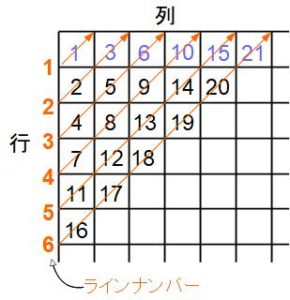
〈特長1〉オレンジ色の斜め線が示すように、1から始まる整数が左下から右上に上がるように配列されています。
〈特長2〉どのオレンジ色の斜め線の終点にも三角数と呼ばれる数が並んでいます。三角数は青い数字で示しました。新しい斜め線は三角数の次の数から始まります。三角数については下の囲みを読んでください。
〈特長3〉オレンジ色の斜め線にラインナンバーをつけると、ライン上のどの整数も「行と列の和」がラインナンバーより1大きくなります。たとえば3行4列の整数19はラインナンバー6上にあり「行と列の和」は3+4=7です。
三角数について
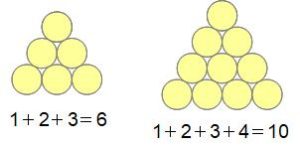
1から順にたした整数の和で表される数を三角数といいます。一番小さい三角数は1で、以下の三角数は次のようになります。
1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
1+2+3+4+5+6=21
以下式は省略しますが、三角数は28 36 45 55 66 78 91 104 120…と続きます。すべて覚える必要はないですが、1から10までの和の55、1から15までの和120など要所要所覚えておくと便利です。たとえば120を覚えておけば1から16までの和も120+16=136とすぐにわかります。
三角数という名前は、これらの数で下のような正三角形が作れることに由来しています。
では設問を考えていきましょう。
(1)
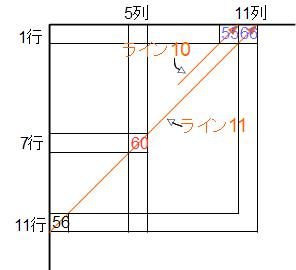
7行5列は「行と列の和」が12です。すると〈特長3〉よりラインナンバー11上にあることがわかります。ラインナンバー11の終点は1から11までたした和(三角数)の66です。7行目にある数は1行目の数より6小さいから、7行5列の数は66-6=60です。
ラインナンバー10の終点55(1から10までの和)を使う手もあるでしょう。ラインナンバー10が55で終われば、ラインナンバー11は56から始まります。7行目にある数は11行目の数より4大きいから、7行5列の数は56+4=60です。
*僕は66や55の場所から行に注目した解説を書きましたが、列に注目してもよいでしょう。どちらかに決めると混乱せずに済みますね。
(2)
数が大きくなっても同じように考えてください。12行18列は「行と列の和」が30です。すると〈特長3〉よりラインナンバー29上にあることがわかります。ラインナンバー29の終点は1から29までたした和(三角数)です。1から整数Nまでの和は次の公式を覚えておくとよいでしょう。
1からNまでの整数の和=(1+N)×N÷2
1から29までたした和(三角数)は (1+29)×29÷2=435 です。12行目にある整数は1行目の整数より11小さいから、12行18列の整数は435-11=424です。
(3)
前の2問と逆に数の位置を特定する設問です。
まず777に近い三角数を考えましょう。それにはある程度調べる作業が必要ですよ。上に書いた公式を使うと1から30までの和が465。これでは足りてませんね。1から40までの和が820。777を少し超えました。820から40を引くと1から39の和になってこれが780。777とはわずかな差だからこの情報が使えそうです。
〈特長2〉からラインナンバー39の終点が780です。ラインナンバー39の終点とは1行39列のことですね。あとは行を1増やし、列を1減らして近づいていくのが手堅いでしょう。
780→1行39列 779→2行38列 778→3行37列 777→4行36列
無事に答えを出すことができました。777は4行36列にあります。
メモ 777は三角数780に近かったですが、もう少し遠い場合はそこでも規則を見つけたいですね。最後に青で書いた部分をよく見てください。行と列の和はすべて40だし、その数と行の和はつねに781です。このことを使えば760の位置を聞かれても21行19列のように求めることができますね。
三角数を使う数表の問題、いかがでしたでしょうか。じつはこうした規則性の問題には唯一無二の解法はなく、僕が示した以外の規則もまだあるでしょう。たとえば1から真下に下げていくと1、2、4、7、11、…となっていて、これは間隔が1、2、3、4、…と増えています。1から右下に下げていけば1、5、13、25、…です。こちらは間隔が4、8、12、…という4の倍数です。このように数表には美しい規則が多く、どの規則を採用するかは悩ましいところもありますね。その中で僕が解説に書いた方法は「行と列の和」がラインナンバーより1大きいという関係がとてもわかりやすいと好評です。行と列がわかればラインナンバーがわかるし、ラインナンバーの終点はすべて三角数だから公式で簡単に求めることができますからね。同じ数表の問題はよく見かけますので、ぜひ覚えておいてほしいと思います。
では新作講座44はこのへんで終わりにしますね。これからも役に立つ算数講座を書き続けますから、ぜひお友だちやお知り合いに口頭でも流行りのSNSでもこの講座を宣伝してやってください。よろしくね。では次の講座でまた算数をいっしょにやりましょう!
みなさんへの宿題
講座の数表をそのまま使ってお考えください。
(1)16行8列の数はいくつですか?
(2)1000は何行何列にありますか?
解答したい方はページ下のコメントに書いてください。正解不正解をレスさせていただきます。お名前はニックネームでもかまいません。













