Newみんなの算数講座9 数学より優秀!?算数の道順たし算

![]()
今回は場合の数の問題としてよく使われる道順問題を解説しようと思います。この考え方には、僕はいまでも算数の知恵の素晴らしさを感じますね。式を立てたり公式に頼ることもありません。とてもユニークな考え方ですよ。
では問題出しますね。
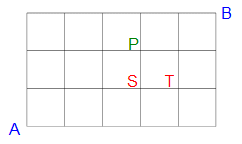
下の図のような道路網があります。
A地点からB地点まで、遠回りをせずに行く最短経路を考えます。
(1)全部で何通りの経路がありますか?
(2)途中、P地点を必ず通ることにすると、 経路は何通りありますか?
(3)ST間が工事中で通ることができないとします。 経路は何通りありますか?
じつはこの問題、「同じものをふくむ順列」という名前で高校数学にも登場します。高校数学では公式を使って計算しますね。(カーテンコール参照)
もちろんそれも一つの方法ですが、僕の感覚ではこの問題については明らかに算数の考え方に軍配ですね。高校数学の計算だと、経路が複雑になったときに式が立てにくくなるのですが、算数の考え方は経路が複雑になっても同じ方法で対応できるのです。講座のタイトルは決して大げさではなく、算数の専売特許ともいえる名解法があります。これならきっと低学年の子供たちでも答えが出せるでしょうね。
では(1)から解説します。
(1)
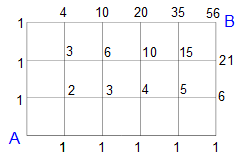
下の図を見てください。それぞれの交差点に数字が書いてあります。
その数字は、スタートのA地点からその地点までの最短経路数を示しています。たとえばAから真上や右方向の交差点へは、どこも直進する1通りの経路しかありません。直進する以外は遠回りになりますからね。各数字は、その交差点をゴールとしたときのAからの経路数という言い方もできます。
Aの近くに2と書いてある交差点がありますが、これは左の1と下の1をたしたものです。つまり、Aから2と書いてある交差点へ行く経路は、左からくる経路(1通り)と下からくる経路(1通り)を合わせて2通りということです。
このように、各交差点の数字は、左と下の数字をたすことで次々に求めていくことができます。左と下の数字がそろってからたし算してくださいね。AからBへ行く経路は全部で56通りが正解です。
(2)
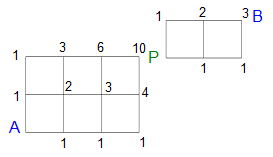
途中のP地点を通る場合は、下の図のように〔スタートAからP地点〕と〔P地点からゴールB〕を分けて考えます。
〔スタートAからP地点〕10通り
〔P地点からゴールB〕3通り
スタートAからP地点まで10通りのどの経路を選んでも、P地点からゴールBまでがそれぞれ3通りずつあるから、P地点を通る経路は10×3=30通りです。
メモ
(1)の答えから(2)の答えを引くと、Pを通らずにAからBまで行く経路数が求められます。(56-30=26通り)
(3)
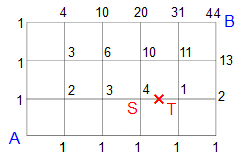
通行禁止区間がある場合は、左の図のようになります。
T地点の数字に注目してください。4+1=5ではなく1になってます。これはST間が通れないため、左のS地点の4がたせないからです。T地点の数字はTの下の交差点と同じ1になります。通れない道の数字はたさないと覚えればよいでしょう。他の部分は(1)と同じように考えて、ST間が通れない場合の経路数は44通りです。
ではオマケにもう一つ。上の問題はきれいな長方形でしたが、こんな形になったらどうしましょう?
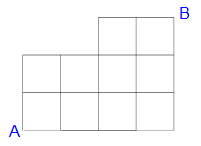
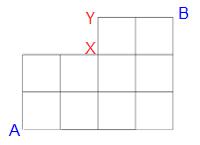
この場合はYの交差点に左からの合流がないから、Yの経路数はXの経路数と同じになります。解答は31通りになりますからみなさんが確認してみてください。
算数ならではの道順たし算、いかがでしたでしょうか。
かつての教え子たちも、高校で習った計算式より算数のやり方がわかりやすくて楽しいと言ってましたね。算数が数学にまさっている? 算数の指導者としては嬉しくなります。中学受験はもちろんですが、大学受験でも就職試験でも算数で解いてはいけないということはないですね。ぜひみなさんも算数の道順たし算を忘れずに覚えておいてくださいね。
では今回はここまでにいたしましょう。
カーテンコール
高校数学では、AからBに行くには右に5マス、上に3マス移動する必要があるから、「右右右右右上上上」という8個の漢字を並べる順列の数として計算します。同じ漢字がふくまれているから8!=8×……×1(通り)ではありません。「右」の重複が5!=5×……×1(通り)、「上」の重複が3!=3×2×1(通り)あるから、8!を〈5!×3!〉で割ることになります。よかったら計算してみてください。
*!→ 階乗。数学記号。その整数から1までの整数をすべてかけた積のこと。
みなさんへの宿題
下の図でA地点からB地点まで、遠回りをせずに行く最短経路は全部で何通りありますか?
解答したい方はページ下のコメントに書いてください。正解不正解をレスさせていただきます。お名前はニックネームでもかまいません。














