NEWみんなの算数講座96 囲碁のような経路数

みなさんこんにちは。ニューみん算講座96回目です。
講座に書く内容ですが、毎回けっこう思案します。ネタはいくら書いても尽きないですが、悩むのは内容よりもレベルですね。簡単な内容が多いと持てあます人が増えるだろうし、難しい内容が多いと敬遠されてしまいますからね。僕としては、算数が得意な人にも得意ではない人にも読んでほしいので、その回ごとに、レベルのメリハリをつけて書いていこうと思っています。
というわけで今回ですが、正直、場合の数の問題でレベルはやや高めです。すごく難しいというわけではないですが、珍しい問題だし、のっている本もあまりないので、知っている人は少ないでしょう。でもじっくりと呼んでもらえれば、算数の素晴らしい知恵を感じてもらえると思います。ではもったいぶらずに問題を紹介しますね。
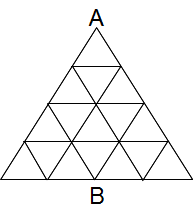
左の図は、1辺の長さが1cmの正三角形を16個組み合わせてできた図形です。点AからBまで正三角形の辺に沿って進むとき、次の長さで進む方法はそれぞれ何通りありますか?
(1)4cm
(2)5cm
問題の意味はおわかりになりますか?
点Aから点Bまで一番早く進むには、4cmで進むことになります。3cm以下ではAからBに到達することはできません。
設問(1)で求めるのは4cmの場合の経路数です。下のような進み方が一例です。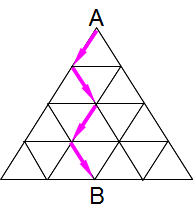
経路数が何通りあるかを正直に数えるのはなかなか大変です。全部の頂点に記号をつけ、A→□→□→□→Bのような樹形図を書いていく方法もありますが、(1)はなんとか正解できても、(2)を正解するのは大変でしょう。たいてい数え忘れが起きそうです。
じつはこの問題には素晴らしいアイデアがあります。それを解説していきますね。
考え方① 「進む長さが1cmだったら?」と考えてみる
進む長さが1cmの場合、点Aのすぐ下にある2個の点(左下と右下)に進む経路があります。1cmではそれ以外の点に進むことはできません。スタートのAに戻ることも1cmでは不可能です。左下と右下の点に1通りずつなので、それを次のように表しておきます。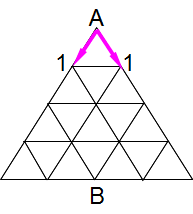
考え方② 1cm延ばして「進む長さが2cmだったら?」と考えてみる
進む長さが2cmになると、1cmのときより一段下の点まで行けるようになります。1cmのときの「1」の点の下にある3個の点まで行けます。
そしてここで大切なのは、1cmのときの図で「1」になっている点や、スタートのAにも、2cmで進むことができるということです。
黄緑色で示した経路は、Aの右下の点へ2cmで進む経路です。また、出発点Aに2cmで進む(AからAに戻る)のは2通りの経路があります。Aから左下に下がって同じ道を戻る経路、右下に下がって同じ道を戻る経路です。この問題には、一度通った道を通れない、同じ点に戻れないという条件はないので注意してください。
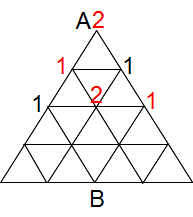
Aから2cmで進める場所は下の通りです。「1」となっている点には1通りの経路があり、「2」となっている点には2通りの経路があります。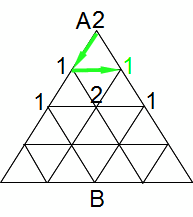
さて、もう1cm延ばして進む長さを3cmにすると、だいぶ話が見えてくると思います。
考え方③ さらに1cm延ばして「進む長さが3cmだったら?」と考えてみる
今度は進む長さが3cmです。2cmのときより、もう一段下の点まで行けるようになります。3cmで到達できない点は、一番下の線上にある5個の点だけです。それ以外の点はすべて3cmあれば到達可能です。
では3cmで進める各点への経路数を示してみます。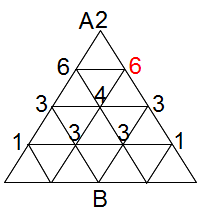
3cmの図を見て、もし次のことに気づいた人がいたら素晴らしく優秀です。
3cmのときの各点への経路数は、2cmのとき、その点から1cm離れていた点の経路数の合計です。
(右側に2cmのときの図をもう一度入れます)
具体例でいきましょう。3cmの図で赤で示した「6」は、2cmの図でその点と1cm離れていた各点の経路数の合計です。
6(←3cmの図)=2+1+2+1(←2cmの図)
理由を説明すると、3cmで「ある点」に到達するためには、2cmのときにその隣の点にいないとならないでしょう?だから3cmのときの6は、2cmのときに隣にあった数の合計2+1+2+1で求めることができるわけです。
ひとつ前の図にさかのぼって考えるというナルホドの考え方ですね。
これで設問(1)の解答は手中です。
Bまで4cmで進む経路数は、3cmのとき、点Bのとなりにある経路数の合計です。3cmのときBのとなりにあるのは左上と右上にある「3」と「3」です。
(1)の解答は3+3=6通りです。
次は設問(2)のBまで5cmの経路ですが、それを考えるには4cmのときの経路数を示しておく必要がありそうです。4cmのときの経路数は次のようになります。どの点も3cmの図でとなりにあった数字をたしています。4cmのときの経路図があれば、Bまで5cmの経路数は簡単です。
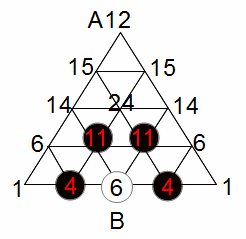
5cmでBに進む経路数は、この図で点Bと隣り合っている点の数をすべて加えます。11+11+4+4=30ですね。(2)の解答は30通りです。
この図の各点でとなりの数をたせば5cmの図もできますが、5cmの図は省略させてもらいますね。この問題が理解できたみなさんは、ぜひ5cmの図も作ってみてください。
*** いかがでしたでしょうか。この考え方を自力で思いつける人は相当の才能の人だと思うし、解説している僕自身もむかし誰かから教わりました。
いかがでしたでしょうか。この考え方を自力で思いつける人は相当の才能の人だと思うし、解説している僕自身もむかし誰かから教わりました。
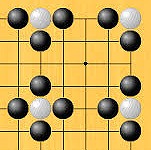
そのとき僕は、この話は囲碁に似てるナと思いました。囲碁を知らない人もいると思いますが、囲碁では右のイラストのように、まわりを黒石で囲まれた白石は取られてしまいます。ある点の経路数を求めるとき、その点自身(白石)を除き、となりの数(黒石)をたす作業が、なんとなく囲碁に思えたのです。それで今回のタイトルを「囲碁のような経路数」にしました。このタイトルでみなさんの記憶にも残ればうれしいです。
では今回の講座はここまでにします。次回97回目の講座を楽しみに待っていてください。次回は久しぶりにベン図を使った集合の話を予定しています。
インフォメーションボード
〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。
〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。
〈算数講座へのご意見や質問/ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。
〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、5講座ずつを1冊子にまとめ、「なかとじ印刷」した片側A5サイズ(開くとA4)のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら













