算数テクニック公式集
よく見かけるものではなく、知らない人が多そうなテクニックや公式を紹介しています。覚えておくと便利なものばかりです。テクニック公式集ですから、ここでは理由にはくわしく触れていません。理由はみなさんが考えてみてください。
テク21 上りの船Aと下りの船Bの速さの和
上りの船Aの速さ=船Aの静水時の速さ-流れの速さ
下りの船Bの速さ=船Bの静水時の速さ+流れの速さ
これらをたすと流れの速さは消える!
上りの船Aの速さ+下りの船Bの速さ
=船Aの静水時の速さ+船Bの静水時の速さ
メモ
流水算で、流れの速さが必要ないパターンとして知られています。
公式テクニック20個到達スペシャル
すいの体積の公式〈底面積×高さ×1/3〉の「×1/3」を算数で説明
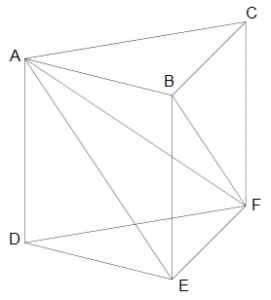
三角柱ABCDEFを使って説明します。
三角すいADEFとABCFで、オレンジの文字で示した面を底面とみると、どちらも三角柱の底面だから面積が等しく、高さのADとCFも等しいから、三角すいADEFとABCFは体積が等しいです。
また、三角すいADEFと三角すいABEFで、赤い文字で示した面を底面とみると、どちらも長方形ADEBの半分だから面積が等しく、高さのEFは共通だから、 三角すいADEFとABEFは体積が等しいです。
これらのことから、三角すいADEF、ABCF、ABEFはすべて体積が等しいことがわかります。つまり三角すいの体積は、底面と高さが等しい三角柱の体積の3分の1になっています。
テク20 ある距離を速さを変えて往復したときの平均の速さ
行きの速さをA、帰りの速さをBとすると、
往復の平均の速さは A×B×2÷ (A+B)
メモ
この式を使うと距離は気にする必要がありません
テク19 軸のまわりを図形が1回転してできる立体の体積
回転図形の面積×回転図形の重心が1回転する長さ(円周)
例 クリーム色の長方形が軸Lのまわりを1回転してできる立体の体積は、長方形の面積に重心Pが1回転する半径5の円周の長さをかけます(パップスギュルダンの定理)
(8×4)×(5×2×3.14)=1004.8
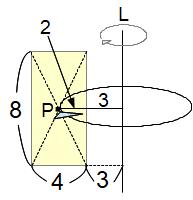
重心 算数では扱わない用語ですが図形のド真ん中と考えてください。
・ 正方形、長方形、平行四辺形、ひし形の重心→対角線の交点
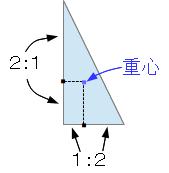
・ 二等辺三角形、正三角形の重心→高さを上から2:1に分ける点
・ 直角三角形の重心→直角の頂点から水平方向に1/3、垂直方向に1/3進んだ点(下図参照)
テク18 素数の個数
トータルとしては無数にあることが証明されています。算数では100までの25個を判断できるようにしておきましょう。
100までの素数(25個)
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,
53,59,61,67,71,73,79,83,89,97
メモ
受験生が素数と間違えることが多い合成数(素数ではない数)は91〈=7×13〉
数学者のグロタンディークが学会で素数と間違えた57はグロタンディーク素数として有名 (57は素数ではありません)
テク17 ある年の★月☆日が□曜日。では翌年の同じ日付の★月☆日は何曜日?
1つ先の曜日。ただし途中にうるう年の2月29日があれば2つ先の曜日。
メモ
うるう年は西暦が4の倍数の年です。ただし400の倍数ではない100の倍数の年はうるう年から除外するという例外があります。(1900年や2100年は平年)
テク16 ある月の★日が□曜日。では翌月の同じ日付の★日は何曜日?
ある月が大の月なら□の3つ先の曜日。小の月(2月以外)なら□の2つ先の曜日。2月と3月の同じ日付は同じ曜日。
メモ
2月 4月 6月 9月 11月が小の月です。「西向くさむらい小の月」と覚えます。11月のさむらいは漢字で書いた11が武士の士に似ているから。小の月でなければ大の月です。
テク15 図形の外周に沿って円が一周(センターラインの定理)
円が通過した部分の面積=円の中心が移動した線の長さ×円の直径
テク14 小数に直せる分数
分母を素因数分解したとき、2と5のどちらかまたは両方で表されていれば小数に直すことができます。(既約分数に限ります)
テク13 選ぶことは選ばないこと
異なるP個のものの中からA個を選ぶ組み合わせの数は、P個から(P-A)個を選ぶ組み合わせの数と等しい。
ヒント 異なる6個の果物から好きな果物を4個選ぶということは、同時に好きではなかった2個も選んでいるのです。
テク12 GL(ガール)の定理
整数P、Qの最大公約数をG、最小公倍数をLとするとP×Q=G×L
テク11 11の倍数の判定方法
一の位からひとつおきの和アと、十の位からひとつおきの和イを求め、アとイの差が11の倍数(0を含む)ならもとの整数は11の倍数
例 整数1903で一の位からひとつおきの和アは3+9=12 十の位からひとつおきの和イは0+1=1 ア-イ=12-1=11(11の倍数)より1903は11の倍数
テク10 BとCの和が10のときのAB×AC
(A+1)×AとB×Cをくっつけます
例 53×57→(5+1)×5 と 3×7をくっつけて3021
テク9 和暦を西暦に直す
令和+2018 平成+1988 昭和+1925 大正+1911 明治+1867
テク8 2から順にたした偶数の和
たした個数×(たした個数+1)
例 2+4+6+8+10=30 → 5×(5+1)
テク7 1から順にたした奇数の和
たした個数×たした個数
例 1+3+5+7+9+11=36 ← 6×6 (たした奇数が6個)
テク6 整数1からNの範囲にあるPの倍数の個数
N÷Pの整数の商 (余りは無視してよい)
テク5 円すいの側面積
母線×底面の半径×円周率
テク4 正N角形の1つの内角の大きさ(第2公式)
180-360÷N(度)
テク3 おうぎ形の面積(裏公式)
半径×弧の長さ÷2
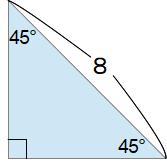 テク2 直角二等辺三角形の面積(裏公式)
テク2 直角二等辺三角形の面積(裏公式)
斜辺×斜辺÷4
*左図の直角二等辺三角形の面積は8×8÷4=16
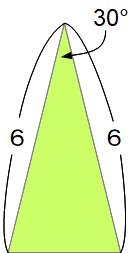 テク1 頂角30°の二等辺三角形の面積
テク1 頂角30°の二等辺三角形の面積
等しい辺の長さ×等しい辺の長さ÷4
*左図の二等辺三角形の面積は6×6÷4=9