NEWみんなの算数講座100 約数の個数別整数リスト

みなさんこんにちは。NEWみんなの算数講座 ついに100回目を迎えました。われながらずいぶん書いてきたものです。

記念の100講座目にあたり、僕がこの算数講座を書いている趣旨を、効果的な算数の勉強方法と関連させて書いておこうと思います。

僕はいろいろな算数の内容を、あまり順番を意識せずに書いてきました。速さなら速さ、食塩水なら食塩水、図形なら図形というように順番に書いてほしいという意見をいただくことがありますが、でも僕は、算数はそういう教わり方で力がつくものではないと思っています。ある週は単元Ａを勉強し、次の週は単元Ｂを勉強し、……とやっていると、そのとき勉強している単元はそこそこできても、通り過ぎた単元のことを次々忘れてしまい、時間をかけた結果、算数の力はあまりついていないということになりがちです。学校も受験の塾もその方法を続けているから、算数ができるようにならない子がたくさんいるのです。

そうした考えがあり、僕はこの算数講座をランダムな内容で書き続けています。ひとつのモノのきめ細かな描写ではなく、僕は算数の風景画を描いているつもりです。海があって空に太陽や雲があって、煙突があって汽車が走っていて鳥が飛んでいて？それがみなさんの頭を刺激する「役に立つ算数講座」だと思っているのです。

算数ができるようになりたい人は、ぜひこの講座を１回から100回まで全編通して読んでみてください。１日２講座読めば２ヶ月かかりませんよ？それによって算数のコツがたくさんわかり、解ける問題が増えて、算数が楽しく感じられて、算数が好きで得意な人になれると思います。

＊web画面は、上げたり下げたり、落ち着いて読むには不便でしょうから、５講座ずつ20冊子に分けたファイルを僕の事務所で製作販売しています。発行以来の販売部数は700部を超えて好評です。手前味噌ですが知恵が詰まったお勧めの算数お宝ファイルです。（説明ページのリンクは一番下にあります）

＊＊＊
珍しく施政方針演説から入ってしまいました(笑)
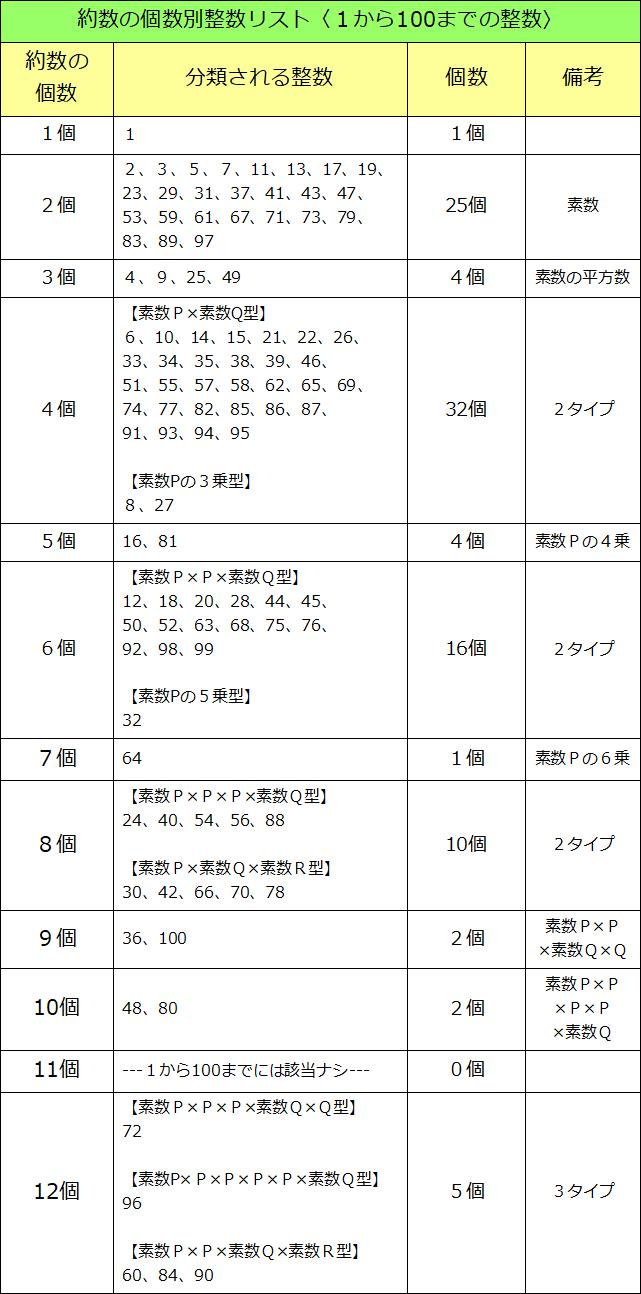
今回の100回目の講座では、最初に書いた１回目の「約数の個数の求め方」の記念続編で、整数を約数の個数別に分類したリストを作りたいと思います。１から100までの整数が11組に分かれます。問題の番号を(…組)と表記しました。組と約数の個数をそろえてあります。では始めますね。

(１組)
約数が１個の整数は１だけです。１の約数は１。これしかありません。正解は１個です。

(２組)
約数が２個の整数は「素数」と呼ばれる整数です。素数の約数は１とその数自身の２個です。
１から100までの範囲にある素数は次の25個です。
２、３、５、７、11、13、17、19、23、29、31、37、41、43、47、
53、59、61、67、71、73、79、83、89、97

(３組)
約数が３個の整数は「素数の平方数」です。平方数とは、同じ数を２回かけた数のことです。たとえば４の約数は１、２、４の３個です。２×２が４だから、約数がダブって１つ消えてしまう感じです。
＊平方数であっても、素数の平方数でなければ約数が３個にはなりません。

１から100までの範囲にある素数の平方数は次の４個です。
４　←　２×２
９　←　３×３
25　←　５×５
49　←　７×７

(４組)
約数が４個の整数は、次のア、イのパターンがあります。

ア「素数□×素数△」でできている整数
たとえば素数２×素数３でできる６には１、２、３、６の４個の約数があります。
このパターンは、１から100までの範囲では次の30個です。
６　←　２×３　　10　←　２×５　　14　←　２×７
22　←　２×11　　26　←　２×13　　34　←　２×17
38　←　２×19　　46　←　２×23　　58　←　２×29
62　←　２×31　　74　←　２×37　　82　←　２×41
86　←　２×43　　94　←　２×47
15　←　３×５　　21　←　３×７　　33　←　３×11
39　←　３×13　　51　←　３×17　　57　←　３×19
69　←　３×23　　87　←　３×29　　93　←　３×31
35　←　５×７　　55　←　５×11　　65　←　５×13
85　←　５×17　　95　←　５×19
77　←　７×11　　91　←　７×13

イ「素数の立方数」
立方数とは、同じ数を３回かけてできる数です。たとえば素数２×素数２×素数２でできる８には１、２、４、８の４個の約数があります。
このパターンにあてはまる整数は、１から100までの範囲では次の２個です。
８　←　２×２×２　　27　←　３×３×３

約数が４個の整数は、アとイをたして32個が正解です。

(５組)
約数が５個の整数は「同じ素数を４回かけた整数」です。
たとえば２×２×２×２でできる16には１、２、４、８、16の５個の約数があります。
このパターンにあてはまる整数は、１から100までの範囲では次の２個です。
16　←　２×２×２×２　　81　←　３×３×３×３

(６組)
約数が６個の整数は、次のウ、エのパターンがあります。

ウ「素数□×素数□×素数▲」でできている整数
たとえば素数２×素数２×素数３でできる12には１、２、３、４、６、12の６個の約数があります。
このパターンにあてはまる整数は、１から100までの範囲では次の15個です。
12　←　２×２×３　　20　←　２×２×５
28　←　２×２×７　　44　←　２×２×11
52　←　２×２×13　　68　←　２×２×17
76　←　２×２×19　　92　←　２×２×23
18　←　３×３×２　　45　←　３×３×５
63　←　３×３×７　　99　←　３×３×11
50　←　５×５×２　　75　←　５×５×３
98　←　７×７×２

エ「同じ素数を５回かけた整数」
２×２×２×２×２でできる32には１、２、４、８、16、32の６個の約数があります。
このパターンにあてはまる整数は、１から100までの範囲では、この32の１個だけです。

約数が４個の整数は、ウとエをたして16個が正解です。

(７組)
約数が７個の整数は「同じ素数を６回かけた整数」です。
２×２×２×２×２×２できる64には１、２、４、８、16、32、64の７個の約数があります。
このパターンにあてはまる整数は、１から100までの範囲では、この64の１個だけです。正解は１個です。

(８組)
約数が８個の整数は、次のオ、カのパターンがあります。

オ「素数□×素数□×素数□×素数▲」でできている整数
たとえば２×２×２×３でできる24には１、２、３、４、６、８、12、24の８個の約数があります。
このパターンにあてはまる整数は、１から100までの範囲では次の５個です。
24　←　２×２×２×３　　40　←　２×２×２×５
56　←　２×２×２×７　　88　←　２×２×２×11
54　←　３×３×３×２

カ「素数□×素数△×素数☆」でできている整数
たとえば２×３×５でできる30には１、２、３、５、６、10、15、30の８個の約数があります。
このパターンにあてはまる整数は、１から100までの範囲では次の５個です。
30　←　２×３×５　　42　←　２×３×７
66　←　２×３×11　　78　←　２×３×13
70　←　２×５×７

「同じ素数を７回かけた整数」も約数は８個ですが、
２×２×２×２×２×２×２でも128なので、同じ素数を７回かけた整数は100以下の範囲にはありません。＊128は約数が８個です。

約数が８個の整数は、オとカをたして10個が正解です。

(９組)
約数が９個の整数は、平方数のうちで、
とくに「素数□×素数□×素数▲×素数▲」でできている整数です。
たとえば２×２×３×３でできる36には１、２、３、４、６、９、12、18、36の９個の約数があります。
このパターンにあてはまる整数は、１から100までの範囲では次の２個です。
36　←　２×２×３×３　　100　←　２×２×５×５

(10組)
約数が10個の整数は「素数□×素数□×素数□×素数□×素数▲」でできている整数です。たとえば２×２×２×２×３でできる48には１、２、３、４、６、８、12、16、24、48の10個の約数があります。
このパターンにあてはまる整数は、１から100までの範囲では次の２個です。
48　←　２×２×２×２×３　　80　←　２×２×２×２×５

＊(８)と同様に「同じ素数を８回かけた整数」は約数が９個、「同じ素数を９回かけた整数」は約数が10個ですが、どちらも１から100までの範囲にはありません。

(12組)
約数が12個の整数は、次のキ、ク、ケのパターンがあります。

キ「素数□×素数□×素数□×素数▲×素数▲」でできている整数
２×２×２×３×３でできる72には１、２、３、４、６、８、９、12、18、24、36、72の12個の約数があります。
このパターンにあてはまる整数は、１から100までの範囲では、この72の１個だけです。

ク「素数□×素数□×素数□×素数□×素数□×素数▲」でできている整数
２×２×２×２×２×３でできる96には１、２、３、４、６、８、12、16、24、32、48、96の12個の約数があります。
このパターンにあてはまる整数は、１から100までの範囲では、この96の１個だけです。

ケ「素数□×素数□×素数▲×素数☆」でできている整数
たとえば２×２×３×５でできる60には１、２、３、４、５、６、10、12、15、20、30、60の12個の約数があります。
このパターンにあてはまる整数は、１から100までの範囲では次の３個です。
60　←　２×２×３×５　　84　←　２×２×３×７
90　←　３×３×２×５

これらを合計して、約数が12個の整数は５個が正解です。

＊＊＊
以上１～100までの整数全員が、11組に分かれ、約数の個数別にリストアップされました。11組の整数の個数を全部たしてみてください。きれいに100個になりますよ？

約数の個数を求める計算方法については、１回目の講座でくわしく書きましたが、素因数分解したときの素数の個数を種類別に調べ、どの個数にも「＋１」をしてかけ算するというものでした。
たとえば18は２×３×３なので、素数２が１個で素数３が２個
➡約数は（１＋１）×（２＋１）＝２×３＝６個です。
16＝２×２×２×２のように同じ素数しか出てこないときは、個数にそのまま１をたして約数は５個です。この仕組みを知っておくと、今回の講座の意味がより鮮明に理解できると思います。

では最後に約数の個数別整数リストを掲載して、今回の講座を終わりにしようと思います。次回から新規一転、また１回目に戻ったつもりで頑張って書いていきたいと思います。あ、受験生のおうちなら、下の表を印刷してどこかに貼っておくと必ず役に立ちますよ。

インフォメーションボード

〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。

〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。

〈算数講座へのご意見や質問／ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。

〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、５講座ずつを１冊子にまとめ、「なかとじ印刷」した片側Ａ５サイズ（開くとＡ４）のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら