算数界の専門用語

ＡまたはＢ　’21年３月４日追加
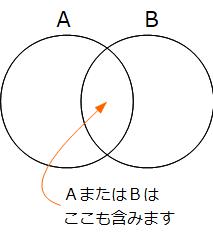算数（数学）で使う「ＡまたはＢ」の表現は、どちらか一方ではなく、両方にあてはまることを含みます。たとえば「偶数または３の倍数」といえば、両方にあてはまる６も含まれます。レストランの注文で「コーヒーまたは紅茶」といえば、それはどちらか一方の選択です。「両方ください」はないでしょう(笑)日常生活と算数（数学）での「または」は意味合いが違うことをおさえてください。

互いに素(たがいに・そ)
２つの整数が１以外の公約数を持たない関係のことです。２つの整数がともに素数のときは互いに素ですが(３と７は互いに素)、必ずしも素数である必要はありません。たとえば９(＝３×３)と20(=２×２×５)は１以外の公約数を持たないから互いに素です。

出題例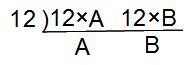
最大公約数が12、最小公倍数が144である2つの整数を求めなさい。⇒２つの整数を12×Ａ、12×Ｂ (Ａ＞Ｂ、ＡとＢは互いに素)とすると、右図の連除法から最小公倍数について
12×Ａ×Ｂ＝144が成り立ちます。この式からＡ×Ｂ＝12です。
Ａ＞ＢでＡとＢが互いに素である(Ａ、Ｂ)の組はア(12、1)とイ(４、３)です。

求める２つの整数は
アの場合→12×Ａ＝12×12＝144 と 12×Ｂ＝12×1＝12
イの場合→12×Ａ＝12×４＝48 と 12×Ｂ＝12×３＝36
解答 144と12 または 48と36
＊Ａ＝６、Ｂ＝２の場合は、６と２が互いに素ではないから、12×６＝72、12×２＝24となり、最大公約数が12ではなくなってしまいます。

内内外外(うちうちそとそと)
比例式Ａ：Ｂ＝Ｐ：Ｑで成り立つ性質Ａ×Ｑ＝Ｂ×Ｐの算数らしい教え方。
「内項の積と外項の積が等しい」を忘れてしまう生徒でもこの覚え方は忘れないらしい。

帯分数(たいぶんすう)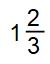
のように整数部分がある分数のことです。
整数と分数の接続部の読みは「と」。むかし「か」と読んでいた時代もあるそうです。おじいちゃんやおばあちゃんに聞いてみよう！
帯分数は仮分数に直すことができ、「1と3分の2」を仮分数に直すと「3分の5」です。(仮分数…かぶんすう。分子が分母より大きいか、分子と分母が等しい分数)
算数では「解答は仮分数ではなく帯分数に直す」が原則ですが、最近の入学試験や大手塾の模擬試験では仮分数の解答を許容することも多いようです。ただしすべての試験で許容される保証はないので、念のため帯分数に直しておくほうが安全運転でしょう。なお、帯分数は算数だけで使われる命の短い分数で、中学以降の数学からは姿を消します。

平均の速さ
いくつかの速さで進んだ行程について、行程全体でならして考えた速さのことです。

たとえば300m離れた2地点間を往路-分速50m、復路-分速30mで往復すると、
進んだ距離は300×２＝600m
所要時間は300÷50＋300÷30＝6＋10＝16分
平均の速さは600÷16＝分速37.5mです。

このように、往復の平均の速さは往路と復路の速さの単純な平均
(50＋30)÷2＝40にはなりません。
＊一発公式もあります。こちらをご覧ください。

木の下で恥をかく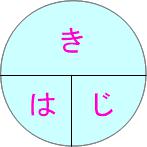
速さの公式を覚えるときの語呂合わせです。どれかの要素を求めるとき、他の２つがタテに残っていたら割り算、並んで残っていたらかけ算です。
はやさ＝きょり÷じかん
きょり＝はやさ×じかん　のように使います

既約分数（きやくぶんすう）
それ以上約分することができない分数のことです。既約の既は訓読みで「すでに」と読みますね。だから文字通りすでに約分が終わっている分数です。たとえば「3/4」は既約分数ですが「3/9」は既約分数ではありません。

倍分（ばいぶん）
約分の反対語。分数の分子と分母に同じ数をかけることです。分数自体の大きさは変わりません。1/2 → 5/10 という感じですね。約分は有名ですが、倍分はあまり知られていないようです。僕のパソコンの変換でも出ませんでした(笑)

3.6倍
秒速○mを時速●kmに換算するときの一発計算。3600倍してから1000で割ることをまとめています。列車の速さの問題（通過算）では必須知識ですね。逆に時速●kmを秒速○mに換算するときは3.6で割ります。

０％の食塩水
水のことです。
食塩水の問題で「水」→「食塩の溶けていない食塩水」→「０%の食塩水」と考える場合があるのです。似た話では、三角形を上底がない台形と考えることがあります。

100％の食塩水
食塩のことです。
上の「０％の食塩水＝水」と同じように、「食塩」→「水がない食塩水」→「100%の食塩水」と考える場合があります。

甲乙丙（こうおつへい）
文章題の中で、ＡＢＣと同じように人や乗り物、場所などの名まえとして甲乙丙の順番に使われることがあります。本来は中国から伝わった十干(じっかん)と呼ばれ、甲乙丙丁戊己庚辛壬癸(こう・おつ・へい・てい・ぼ・き・こう・しん・じん・き)の順に10個あります。これらを十二支と組み合わせ、六十年をひと回り（還暦）とする十干十二支は有名ですよ？
余談ですが、私は乙＋巳(み年)＝乙巳(きのとみ)、令和３年度の六年生は平成21年４月～12月生まれなら己＋丑(うし年)＝己丑(つちのとうし)、平成22年１月～３月の早生まれなら庚+寅(とら年)＝庚寅(かのえとら)です。算数では甲乙丙まで知っていれば十分です。

たして求める差
算数にマイナスの数がないことによって生じる独特の言い回しです。たとえば、学校の始業時間に対して「12分早く着くこと」と「８分遅れること」の差は12＋８＝20分です。12－(－8)＝20と考えれば引き算の差ですが、算数にはマイナスの数がないから、反対語の差はたして求めると教えます。「毎分10Lの給水」と「毎分５Lの排水」の差が10＋５=15Lになるなども同様です。