Newみんなの算数講座２ 約数の総和の求め方

前回は約数の個数を求めましたが、今回はそれを応用させて、約数の総和の求め方について考えてみることにしましょう。

この方法を知っている人は、算数を勉強している人のごく一部だと思います。
ほかの人が知らないことを先に知る！
算数に対する自信ってそんなところから芽生えたりするんですよね。期待して読んでくださいね。

約数の総和というのは、約数をすべて合計するといくつになるか？ということです。

では、次の問題を考えてみます。

前回の黒板にも書きましたが、７２は１００以下の整数では約数の個数が最多の１２個あります。
（６０ ７２ ８４ ９６が四者首位タイ）
１２個ならさくらんぼ方式でも書けないことはなさそうですね。

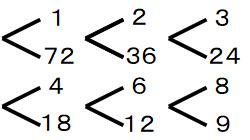
今回のテーマは、これらの総和を求めることです。

まずは自力でたしてみましょうか。紙に書いて、たした数を消したりしながら、上手にたしてみてください。なるべくピッタリになるように組み合わせるのがいいかな。
一例を示しますね。
（７２＋１８）＋（３６＋２４）＋（１２＋８）
＋（９＋１）＋（６＋４）＋（３＋２）
＝９０＋６０＋２０＋１０＋１０＋５＝１９５

自力で答えを出すことができました。１９５が正解です。

しかしもっと大きい整数で約数の個数が多くなると、さくらんぼ方式も大変だし、実物の約数を書き出してダイレクトにたすのは簡単ではないでしょう。

じつは約数の総和も簡単な計算で求めることができるのです。

ではさっそくやり方を説明します。手順１は前回と同じです。

ではこの方法の理由を説明することにします。
説明には次のような約数マトリックスという表を使います。

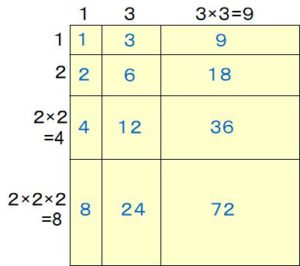
黒い数字はそれぞれのマス目のタテや横の長さです。タテは素数２の使い方を長さで区別し、横は素数３の使い方を長さで区別しています。

タテの長さ、横の長さが決まれば約数が決まります。マス目は全部で１２個ありますね？マス目の数が７２の約数の個数になっています。

たとえば２を１個、３を１個使えば、２×３＝６という約数になり、２を２個、３を１個使えば、２×２×３＝１２という約数になります。
マス目の中の青い数字が７２の具体的な約数です。タテと横をかけた長方形の面積が、ひとつひとつの約数を示しているわけですね。

ここで注意したいのは、素数２と３の片方だけを使っても約数はできるから、タテ、横ともに長さ１の線があります。８という約数は（２×２×２）×１ということですね。さきほど手順２でたした１はこの意味だったのです。
＊素数２と３を両方使わなければ１×１＝１という約数になります。

あと一歩です。
７２の約数の総和は、上の表全体の面積だから、
表全体のタテの長さ　１＋２＋４＋８＝１５
表全体の横の長さ　１＋３＋９＝１３
タテの長さと横の長さをかけて、７２の約数の総和は無事に
１５×１３＝１９５となります。

約数マトリックスを用いた約数の総和の求め方、楽しんでいただけたでしょうか？
鋭い人はお気づきになったかもしれませんが、整数を組み立てている素数が３種類以上になると、平面での説明はできなくなりますね。その場合は立体かな。４種類以上だと立体も無理ですね。でも安心してください。素数の種類が何種類になっても、同じ方針で大丈夫ですから。

＊今回の講座の復習テストが講座106にあります。

インフォメーションボード

〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。

〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。

〈算数講座へのご意見や質問／ウタマル先生へのお便り〉
どうぞこちらのフォームからお寄せください。

〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、５講座ずつを１冊子にまとめ、「なかとじ印刷」した片側Ａ５サイズ（開くとＡ４）のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら