Newみんなの算数講座１ 約数の個数の求め方

Newみんなの算数講座の記念すべき第１回は、整数問題のジャンルから、約数の個数の求め方についてお話をしたいと思います。

まず簡単に約数のおさらいをしておきましょう。約数とは、ある整数を整数の範囲で割りきれる数のことです。具体的に書いたほうがわかりやすいでしょう。

８の約数　 １　２　４　８
２０の約数　１　２　４　５　１０　２０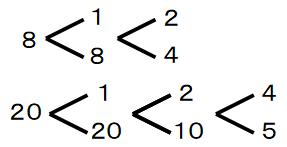

このように小さい約数を思いついたら、積が８や２０になるように、対になる約数も同時に書いていくとよいでしょう。さくらんぼ方式という名前をつけてくれた生徒がいましたよ？
８には４個の約数があり、２０には６個の約数があります。

では、次の問題を見てください。

１　２　３　４　５　６　８　・・・・・

かなりいっぱいありそうですよ？
根気よく書いて調べていけば、なんとかわかるかもしれませんが、それはかなり疲れそうですね。

さくらんぼ方式？
確かにいい方法ではあるのですが、この場合は約数の個数がけっこう多いから、途中で何かを抜かしてしまう可能性もありそうです。さくらんぼ方式を使っても、かなりの注意深さと辛抱強さが必要でしょう。

そこで今回のテーマ。
約数の個数を計算式で求めることはできないだろうか？
これができたら嬉しいですよね。期待感が高まってきましたか？
はい。ちゃんとできるんですよ。

ではやり方を解説しますから、しっかり読んでください。

では、さきほどの方法の理由についても説明しておきます。
約数とは、素因数分解したときに現れる素数（３６０を組み立てている部品）を、いろいろな組合せでかけ算することによって作ることができます。

たとえば３６０は２が３個、３が２個、５が１個という部品からできていますが、その一部（または全部）を使ってかけ算を行うと、
（２×２）×３＝１２
（２×２×２）×５＝４０
のように３６０の約数を作ることができるのです。
つまり、３６０を組み立てている素数を使って、かけ算してできる積のパターンが何通りあるか？
そのパターンの数が約数の個数ということになりますね。 かけ算をせず、どれかの素数を単独で考えても約数です。

そこで、かけ算するときに、それぞれの素数の使い方が何通りあるかを考えると、
２という素数は
３個使う　２個使う　１個使う　０個使う　→４通り

３という素数は
２個使う　１個使う　０個使う　→３通り

５という素数は
１個使う　０個使う　→２通り

ここで場合の数の考え方を使いますが、２の使い方が４通り、３の使い方が３通り、５の使い方が２通りあるから、これらを組み合わせてできるかけ算のパターンは４×３×２＝２４（通り）
したがって３６０の約数の個数を２４個と求めることができるわけです。

あ、ボクが書く前に気づいた人がいるみたいですね。そう、手順３でそれぞれ１をたしたのは、その素数の使い方に、０個使う（使わない）という使い方があるからです。また、どちらの素数も使わない場合は１という約数が生まれます。

どうですか？今回の内容は理解してもらえましたか？
素因数分解を利用して約数の個数を求めるテクニック楽しいでしょう？
この話をさらに広げていくと、約数マトリックスというユニークな図形の話もあるのですが、それは次回の講座でお話することにしますね。

＊今回の講座の復習テストが講座106にあります。

インフォメーションボード

〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。

〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。

〈算数講座へのご意見や質問／ウタマル先生へのお便り〉
どうぞこちらのフォームからお寄せください。

〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、５講座ずつを１冊子にまとめ、「なかとじ印刷」した片側Ａ５サイズ（開くとＡ４）のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら