Newみんなの算数講座42 車と上り下りの電車の関係

お待たせしました。新しい講座できました。
講座42は前回と同じ速さがテーマです。全体では講座７、18、19、25、41と今回だから６回目の速さですね。速さは例年中学入試の八割の学校で出題される超重要テーマなので、僕も積極的に取り上げています。
今回は運行間隔の問題を選びました。とっつきにくさを感じてなかなか理解できない人が多いようです。確かに他の速さの問題とは様子がちがうんですよね。でも一度コツをつかめば困らなくなると思いますよ。ではさっそく問題を出してから解説することにしましょう。

運行間隔の問題とはこういう問題です。

この問題は与えられた数値が少ないのが特長です。12分と20分しかありませんね。でもそのことから、それほど複雑な式にはならないのではないか？という予想ができますよね。実際その予想は当たってますよ。この問題は考え方を手中にすれば答えを出す手順は簡単です。

まず、問題の状況を図に表してみましょう。

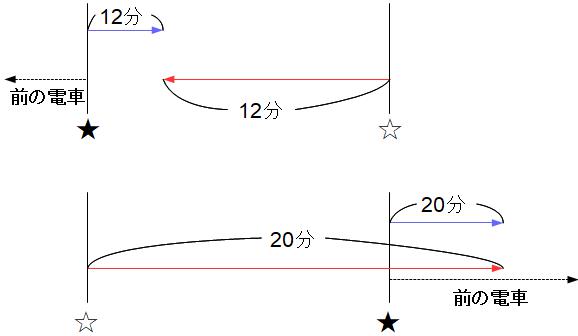
図上はクルマと上り電車の関係です。
★の位置でクルマ(青い線)と前の電車(黒い点線)がすれ違ったあと、次の電車(赤い線)とすれ違うまでに12分かかることを表しています。★の位置でクルマと前の電車がすれ違ったとき、次の電車は☆の位置にいました。つまりクルマは★から12分、次の電車は☆から12分進んですれ違います。
＊点線で示した前の電車は書かなくても大丈夫です

図下はクルマと下り電車の関係です。
★の位置でクルマが前の電車に追い越されてから、次の電車に追い越されるまでに20分かかることを表しています。★の位置でクルマが前の電車に追い越されたとき、次の電車は☆の位置にいました。つまりクルマが★から20分走ったとき、☆から20分で走ってきた次の電車に追い越されます。

(1)
２つの図に共通しているのは、前の電車が★の位置にいたとき、次の電車が☆の位置にいたことです。上りも下りも同じ間隔で走ってますから、２つの図の★と☆の距離は等しいです。
★と☆の距離は、図上ではクルマが12分で走った距離と電車が12分で走った距離の合計、図下では電車が20分で走った距離とクルマが12分で走った距離の差です。
ここでクルマの分速を１、電車の分速を１とすると次の式が成り立ちます。
12＋12＝20－20
両辺に20をたして右辺の－20を消します。
12＋12＋20＝20－20＋20
32＋12＝20
両辺から12を引いて左辺の＋12を消します。
32＋12－12＝20－12
32＝８
両辺を８で割って
４＝１

〈速さの重要知識〉距離が等しいとき、所要時間と速さの比は逆比になります

キーボード入力の都合で２つの比を色を変えて表示しましたが、みなさんは○の比と□の比で表現してくださいね。最後の式はクルマが４分で走る距離と電車が１分で走る距離が等しいことを意味するから、クルマと電車の速さの比は１：４とわかります。

(2)
電車の運行間隔とは、前の電車と次の電車の間隔を電車が何分で走るかということです。
電車と電車の間隔は、さきほどの図に示した★と☆の距離です。上下どちらの図で考えても大丈夫ですが、上の図で考えるなら、クルマが12分で走る距離を電車は３分で走ります(電車の所要時間はクルマの所要時間の1/4)。すると★と☆の距離を電車が走ると３＋12＝15分かかりますね。この15分が電車の運行間隔です。下の図で考えても同じです。クルマが20分で走る距離を電車は５分で走るから、★と☆の距離を電車が走ると20－５＝15分かかります。

運行間隔の問題、理解してもらえたでしょうか。一度で難しければ二度、三度読んでみてくださいね。パソコンやモバイルでながめるだけではなく、プリントしてペンやノートも使って確認しながら読むことをお勧めしますよ。

では今回はこのへんで……にはまだしません！(*^^)
じつはこの問題には速さの比を一発で求める公式があるんです。いつも講座を読んでもらってますからね。僕からのお礼で紹介しちゃいましょう。覚えておくと便利ですよ。

え？この公式だけでいいって？ 僕は理由を知らずに公式だけ覚えるのは反対かな。ズバリ同じ問題ならいいけど、形が変わったときに棒暗記は通用しないからさ。解説した理由をわかった上で一発公式も覚えてくれたら鬼に金棒だと思います。

では今度は今回はこのへんで……にします(笑)
また次の講座でいっしょに算数を勉強しましょう。元気でね！