Newみんなの算数講座69 ワワルワ、ワワルサ

みなさんこんにちは。ニューみん算講座69です。

今回は列車が主役の通過算をテーマに選びました。通過算といえば流水算、時計算と並んで速さの文章題のスリートップの一員です。でもなぜか今まで書いてなかったです。自分でも意外でしたけど今回講座69に通過算の初登場です。

通過算とは、列車が電柱や人の前を通過したり、駅のホームやトンネルや鉄橋を通過する速さの問題のことです。通過するから通過算。そのまんまのネーミングですね。
人や電柱などの横幅は考えないとか、ホーム、トンネル、鉄橋等を通過するときは、通過物の長さに列車の長さを加えたものが走行距離になるとか、通過算にはいくつかの常識があります。

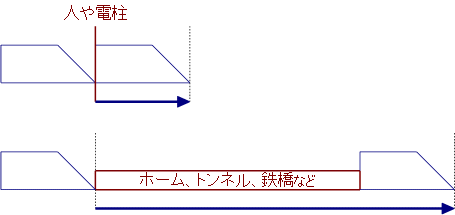
下の図を見てください。
横幅を考えない人や電柱の前を通過するとき、列車が走る距離は〈列車の長さ〉そのものです。また、ホーム、トンネル、鉄橋などを通過するときに列車が走る距離は〈通過物の長さ＋列車の長さ〉です。

ではここまでの内容で解ける問題を出してみます。

通過算に慣れてくれば式だけで済ますことも十分できると思いますが、ここでは図を示して解説します。

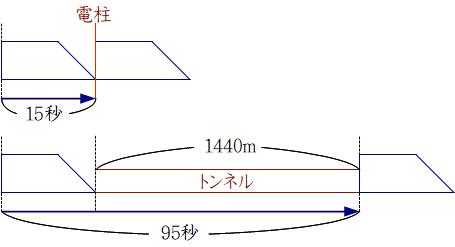
上の図のように、電柱の前を通過するとき、列車が走る距離は〈列車の長さ〉です。トンネルに入り始めてから出終わるまでに列車が走る距離は〈列車の長さ＋トンネルの長さ〉です。
図には列車の最後尾の移動距離を矢印で示しましたが、上下の移動の差は〈トンネルの長さ〉の1440mで、その移動に要した時間は95－15＝80秒です。このことから列車の速さは1440÷80＝18m/秒とわかります。

列車の長さは列車が15秒で走る距離だから、18×15＝270mです。

この列車が1080mの鉄橋を渡り始めてから渡り終わるまでに走る距離は〈列車の長さ＋鉄橋の長さ〉だから、その所要時間は
(270＋1080)÷18＝75より、75秒→１分15秒です。

ここまでが通過算の基本中の基本でした。では次にすれ違いと追い越しについて解説したいと思います。まずすれ違いから。

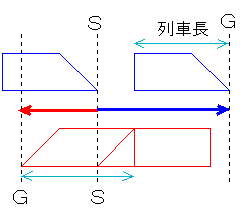
反対方向から来る青、赤２つの列車があって、上の図のＳ地点ですれ違いが開始されました。青い列車と赤い列車の先頭部分が一致していることを確認してください。すれ違いが終わるのは、それぞれの列車の先頭がＧ地点まで進んだときです。そのとき２つの列車の最後尾が一致していることを確認してください。
さて、青い矢印で示した部分が青い列車の進んだ距離、赤い矢印で示した部分が赤い列車の進んだ距離です。両方の矢印をたすとどうなりますか？ ちょうどぴったり２つの列車の長さの和になってますね。

このように列車のすれ違いでは、すれ違いが始まってから終わるまでに、２つの列車の進んだ距離の和が２つの列車の長さの和に一致します。また、２つの列車は向き合って進んでいるから、単位時間あたり、速さ(通過算では秒速が多い)の和の分だけ２つの列車は近づくことになり、そのことから次のような公式が作れます。

次は追い越しです。

同じ向きに走る２つの列車があって、上の図のＳ地点で追い越しが開始されました。青い列車の先頭部分が赤い列車の最後尾に一致していることを確認してください。追い越しが終わるのは、それぞれの列車がＧ地点まで進んだときです。青い列車の最後尾が赤い列車の先頭部分に一致していることを確認してください。すれ違いのときと同じように、青い矢印で示した部分が青い列車の進んだ距離、赤い矢印で示した部分が赤い列車の進んだ距離です。青い矢印から赤い矢印を引くとどうなりますか？ 今度もぴったり２つの列車の長さの和になっています。

このように速い列車が遅い列車を追い越すとき、追い越しが始まってから終わるまでに、２つの列車の進んだ距離の差が２つの列車の長さの和に一致します。２つの列車は同じ方向に進んでいるから、単位時間あたり、速さの差の分だけ速い列車が遅い列車に追いつくことになり、このことから次の追い越し公式が作れます。

ではすれ違いと追い越しの問題を１問ずつ。公式を使えば簡単ですよ。

(1)
まず時速〇kmを秒速●mに直します。１時間は60×60＝3600秒だから、時速は3600で割れば秒速になります。
[特急]　時速108km＝時速108000m
108000÷3600＝1080÷36＝秒速30m
[急行]　時速72km＝時速72000m
72000÷3600＝720÷36＝秒速20m

メモ　これらの計算をひとまとめにし、時速〇kmを秒速●mに直すときに3.6で割るという方法があります。逆に秒速●mを時速〇kmに直すなら3.6倍です。

すれ違い公式を使って、
(200＋150)÷(30＋20)＝350÷50＝７より、特急列車と急行列車のすれ違いには７秒かかります。

(2)
追い越し公式を使って、
(200＋150)÷(30－20)＝350÷10＝35より、特急列車が急行列車を追い越すには35秒かかります。

ワワルワ、ワワルサの呪文で覚える通過算公式いかがでしたか？ どうせ覚えなくてはならない公式なら楽しく覚える方が良いと思います。ただ、公式というのは なぜそうなるのか？ を知らずにただ暗記するだけでは、そのまま公式が使える問題以外での応用がきかなくなってしまうから注意してくださいね。この講座で書いた公式の理由も知っておいてほしいですよ。

では今回の講座69は以上です。次回の講座70は新作No.9になると思いますが、どのような内容を書くか現在考え中で未定です。なのでいま予告はできないですが、発表まで楽しみに待っていてくださいね。じゃあそれまでみなさんお元気で～！

カーテンコール
公式を楽しく覚えてもらうのは僕の算数の流儀でもありますが、それは算数の敷居を低くして算数を好きになってほしいからです。だけど公式を覚えておしまいという算数はやはり行き詰まるんですよね。通過算の場合でも、ホームを通過するときに列車が走る距離は〈ホームの長さ＋列車の長さ〉ですが、これは列車の先頭がホームにさしかかってから最後尾が抜けるまでという状況下に限定され、列車の最後尾が進入してから先頭が抜けるまでという状況下なら〈ホームの長さ－列車の長さ〉が走行距離です。公式もいいですが、同時に積極的に図を書く算数を心がけてくださいね。