Newみんなの算数講座70 比をそろえる、比を作る

みなさんこんにちは。いつもアクセスをありがとうございます。
ニューみん算講座70回目は新しい講座を書くことにしました。ご存知ない方も多いと思いますが、こちらのNewみんなの算数講座は、別のサイトで書いてきた講座をより良い内容に改定して発表しています。著者としてはできるだけ昔の講座を残したいのですが、アクセス数のデータを見て、あまり人気がなかった回は新作に取りかえています。そんなわけで今回はニューになってから９個目の新作講座です。

今回の新作講座のテーマは比です。算数では重要な役割を果たす解法ツールの比ですが、中高の数学では算数ほど使う機会がないから、だいぶ算数に寄った概念と言えるでしょう。頭が算数になじんでいないとうまく使えない傾向もあるようです。

それでは算数での比の上手な使い方を４つの問題で解説します。
まずは１問目。この問題で比を使わなかったらいつ使う？というぐらい比が活かせる問題です。

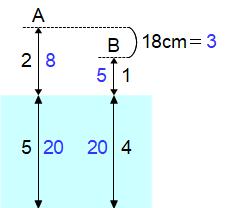
黒い数字に注目してください。Ａの棒は全体の2/7が水面より上に出たから、水中にあるのは5/7で、これらを整数の比で表すと２：５です。Ｂの棒は全体の1/5が水面より上に出たから、水中にあるのは4/5で、これらを整数の比で表すと１：４です。
この２種類の比は違う種類の比だから直接の比較はできません。そこで池の深さを５と４の最小公倍数20にそろえます。すると左側の比は２：５を４倍して８：20になり、右側の比は１：４を５倍して５：20になります。
するとＡとＢの長さの差は３になり、これが18cmにあたるから、１＝18÷３＝６cm。池の深さは20だから、６×20＝120cmと求めることができます。

メモａ　このような作業を算数では〈比をそろえる〉といいます

メモｂ　比は１：２→３：６ (３倍した) のように前後に０以外の同じ数をかけても、12：８→３：２ (４で割った) のように前後を０以外の同じ数で割ってもかまいません。このようにしてできる比を等しい比といいます。状況に応じて等しい比を作ることは算数ではとてもよく行う手段です。

続いて２問目です。

(1)
10円玉と50円玉の枚数の比から、それぞれの合計金額の比を作ります。比に慣れていない人は、この〈新しい比を作る〉という作業が思い浮かびにくいようです。
５：３は具体的な枚数ではなく枚数の比ですが、この比を１枚の単価にかければ合計金額の比を作ることができます。

10円玉の合計金額：50円玉の合計金額
＝(10×５)：(50×３)＝50：150＝①：③

この①：③の合計は④で、それが1000円にあたるから、
①にあたる金額は 1000÷４＝250円 です。
10円玉の合計金額＝①＝250円
50円玉の合計金額＝③＝250×３＝750円

10円玉の枚数は 250÷10＝25枚
50円玉の枚数は 750÷50＝15枚
よって求める解答は 25＋15＝40枚 です。

メモ　解答に直結するような重要な比は、解説のように〇で囲むと比であることがより明確になってわかりやすくなります。重要な比がいくつかあるときは〇→□→△というようにマークを変えていくとよいでしょう。

(2)
100円玉と500円玉の合計金額の比を１枚の単価で割ってそれぞれの枚数の比を作ります。

100円玉の枚数：500円玉の枚数
＝(４÷100)：(５÷500)＝0.04：0.01＝④：①

この④：①の合計は⑤で、それが35枚にあたるから、
①にあたる枚数は 35÷５＝７枚 です。
100円玉の枚数＝④＝７×４＝28枚
500円玉の枚数＝①＝７枚

求める全部の金額は 100×28＋500×７＝2800＋3500＝6300円 です。

メモ　(４÷100)：(５÷500) の計算で１枚の金額はそのまま使いましたが、100円：500円を１：５に直してから割り算しても同じことです。

このようにかけ算や割り算で新しい比を作る感覚をぜひマスターしてください。かけるか割るかは、具体的な量の場合と同じように考えれば大丈夫です。この点については講座23のオマケの知識でも説明しています。

３問目にいきましょう。

絶対だめとは言いませんが、Ａ君やＢ君の具体的な速さは求めるのは上手な方法ではありません。なぜなら数値が悪くてどちらの速さも下のような扱いにくい分数になってしまうからです。

〈やりたくない計算〉
Ａ君の速さ→300ｍ÷58秒＝150/29 (ｍ/秒)
Ｂ君の速さ→300ｍ÷72秒＝25/6 (ｍ/秒)

もちろんこの分数の速さを使って考えていくこともできますが(カーテンコール参照)、やはり速さがこのような分数になるとわかった時点で違和感を感じるべきでしょう。比を使ったおススメの解き方を書きますね。

Ａ君とＢ君は同じ距離(300ｍ)を走るのにかかる時間が58秒と72秒だから、その比を考えると
58秒：72秒＝29：36 です。

距離が等しいとき、所要時間の比と速さの比は逆比になるから、二人の速さの比は 36：29 です。
いま、二人の秒速をそれぞれ36、29と考えると、
Ｂ君が先に走った７秒で進む距離は 29×７秒＝203 です。

この距離をＡ君が追いかけていくと、１秒あたりに追いつく距離は 36－29＝７ だから、203を追いつくまでにかかる時間は 203÷７＝29秒です。
＊ここでは比を緑色にしましたが、みなさんが書くときは数字を〇で囲んでください。数字が大きな〇数字が入力できないのです。製作事情(*´з`)

Ａ君は58秒でトラック１周(300ｍ)するから、その半分の29秒では300÷２＝150ｍ走ります。これが解答です。

メモ　最後のところで29秒が58秒の半分だったので300÷２＝150ｍという近道をしましたが、どのような秒数でも「58秒で300ｍ」と比例式で比べれば秒速を使わずに距離が計算できます。58秒：29秒＝300m：□mといった要領です。

このように考えると、分数になる秒速を使わずに整数の範囲で解決しています。算数に慣れていない人は「二人の秒速を36、29と考える」という前提がなかなか持ち出せないようです。それはおそらく36、29という秒速が、〇m/秒のように距離の単位がついた具体的な速さではないからでしょう。確かに秒速36、秒速29という速さ(正確には速さの比)には距離の単位がありません。しかし、その無単位の秒速に７秒という具体的な時間をかけた距離を、もう一度無単位の秒速の差で割れば、そこで出てくるのは29秒という具体的な秒数です。こうした比の操作に慣れてくると算数がますます面白くなると思います。

最後の１問。図形の問題です。

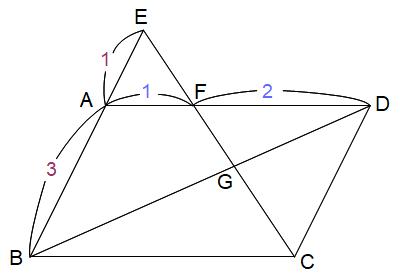
目がチカチカするかもしれませんが、相似な三角形をオレンジとグリーンで囲み、複数の比は色を変えて区別してみました。
△ＥＡＦと△ＣＤＦは相似で、ＥＡ：ＤＣ＝１：３だから、ＥＦ：ＦＣも１：３です。
△ＦＧＤと△ＣＧＢも相似で、ＦＤ：ＢＣ＝２：３だから、ＦＧ：ＧＣも２：３です。
この１：３と２：３は基準がちがう別の比だから、ＦＣを15とすることで二つの比を統一します。
１：３は５倍して５：15
２：３は合計が15になるように３倍して６：９です。
このことで二つの比はピンク色の比にそろえることができています。

ＥＦ：ＦＣ：ＧＣ＝５：６：９が正解です。

メモａ　15の根拠はＦＣを示す３と５の最小公倍数です。このように二つの比をそろえるときは共通部分を最小公倍数にします。

メモｂ　ＥＣ＝１と考え、ＥＦを1/4、ＦＧを3/4×2/5＝6/20、ＧＣを3/4×3/5＝9/20のように分数で表し、1/4：6/20：9/20を整数比に直して５：６：９という手もあります。ＦＣ＝１でもよさそうですね。いろいろできますが、僕はこうした比合わせは最小公倍数の利用をお勧めします。

４問続けて比を使うことできれいに解ける問題を解説しました。しっかり理解できましたか？
中高の数学ではｘ、ｙといった文字を多用して問題を考えることが多いですが、算数ではｘ、ｙの利用をできるだけ抑える代わりに、比がとても重要な解法ツールになっています。比を制する者が算数を制すると言っても大げさではないでしょう。比が使える問題では積極的に比を使ってみてくださいね。この講座でもまた別の機会に比の使い方を追加したいと思ってます。

では今回の講座70はこれで終わりにします。次回の講座71も連続の新作を書いて発表しますよ。テーマは場合の数です。楽しみに待っていてくださいね。じゃあそのときにまた～！(^^♪

カーテンコール
３問目の速さの問題で比を使わない解法は次の通りです。速さがもっときれいな数値ならこちらも全然ありでしょう。しかしこの場合は速さの差の分母が174になります。避けたいでしょう？(^^♪
Ａ君の速さ→300ｍ÷58秒＝150/29 (ｍ/秒)
Ｂ君の速さ→300ｍ÷72秒＝25/6 (ｍ/秒)
Ｂ君が先に走った７秒で進む距離は、25/6 (ｍ/秒)×７秒＝175/6(ｍ)
この距離をＡ君が追いかけていくと１秒あたり150/29－25/6＝900/174－725/174＝175/174(ｍ)追いつくから、175/6(m)追いつくまでにかかる時間は175/6÷175/174＝29秒 です。この時間でＡ君が走る距離は150/29 (ｍ/秒)×29秒＝150(ｍ)です。