Newみんなの算数講座64 時計算の初歩

今日も算数知恵宝庫にようこそ~。ニューみん算講座64です。
元祖の講座64はボツ(不採用)にしまして、今回はニュー講座になって7つめの新作、内容は時計算です。時計算はいままであまり書いたことがなかったですよね。講座43でシャドー針のことを書きましたが、あれはわりと難しめな時計算でしたからね。今回はもう少し基本的な時計算を解説しようと思います。与えられた時刻の角度を求める問題、長針と短針が重なる時刻、直角になる時刻を求める問題を選びました。では順番に出して解説していきますね。
次の時刻の長針と短針が作る角度を180°より小さい方の角度で答えてください。
(1)9時20分
(2)5時47分
有力な考え方が二つあります。一つはズバリその時刻の図を書いて考える方法。もう一つは〇時ちょうどというピッタリの時刻に戻し、長針が短針を追いかける旅人算として考える方法です。(1)を前者、(2)を後者で解説しますね。
その前に次のポイントは時計算でよく使うことなので、これはその都度計算するのではなく知識として覚えてしまってください。
時計の長針と短針の速さ(角速度)
長針(分針)は分速6° → 60分で360°(1回転)進むから、360°÷60分=分速6°です。
短針(時針)は分速0.5° → 60分で30°(文字盤の数字の1マス)進むから、30°÷60分=分速0.5°です。
*時計算にはこれらの差の5.5°を使う問題がとても多いです。応用問題では和の6.5°を使うこともありますね。
(1)
ズバリ9時20分を書いて考えます。
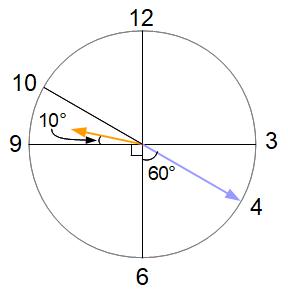
長針はピッタリ数字「4」を指し、短針は分速0.5°だから数字「9」から0.5°×20分=10°進んだ位置を指します。数字「4」から数字「9」の角度が60+90=150°、それに10°を加えて、9時20分の角度は160°です。
設問(1)は長針が数字の方向をピッタリ指すからズバリの図でも良いと思います。設問(2)は長針が半端な方向を指すから別の考え方をしてみます。
(2)
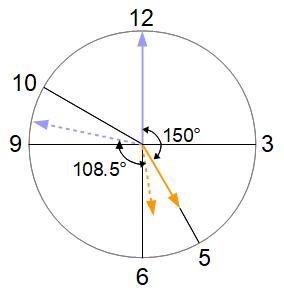
5時ちょうどに戻して、長針が短針を追いかけていく旅人算として考えます。
5時ちょうどの長針と短針の角度は30°×5=150°です。その後1分たつごとに長針は短針に6-0.5=5.5°ずつ追いついていきます。すると47分では5.5×47=258.5°追いつきます。この角度は初めの150°を超えているから、長針は短針に追いついて追い越すことになります。追い越す角度は258.5°と150°の差の108.5°で、これが5時47分の角度です。
では次の問題です。
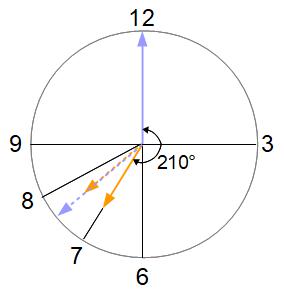
7時台で時計の長針と短針が重なるのは7時何分ですか?
7時ちょうどの長針と短針の角度は30°×7=210°です。その後1分たつごとに長針は短針に5.5°ずつ追いついていくから、210°追いつくのにかかる時間は210÷5.5=210/5.5=420/11=38と2/11分です。求める時刻は7時38と2/11分です。
メモ1 210/5.5の分母と分子を2倍して420/11と直しました。
メモ2 問題が何分何秒まで要求している場合は、2/11分を60倍して120/11秒=10と10/11秒とします。7時38分10と10/11秒です。
もう一問いきましょう。
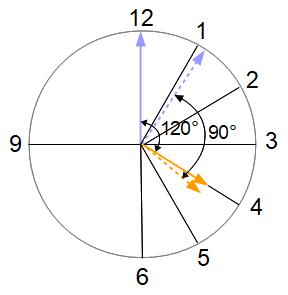
4時台で時計の長針と短針が直角になるのは4時何分ですか? 答えは二回あります。両方とも求めてください。
4時ちょうどの角度は30°×4=120°です。
この角度が直角になる1回目は、長針が短針より120-90=30°多く動いたときです。長針が短針より30°多く動けば、初めの120°差が直角の90°差に減りますね。
長針は短針より1分間に5.5°多く動くから、30°多く動くのにかかる時間は30÷5.5=30/5.5=60/11=5と5/11分です。求める1回目の時刻は4時5と5/11分です。
2回目に直角になるのは、長針が短針より120+90=210°多く動いたときです。長針が短針より210°多く動くと、長針は短針に追いついて追い越し、その差が直角の90°になります。
長針は短針より1分間に5.5°多く動くから、210°多く動くのにかかる時間は210÷5.5=420/11=38と2/11分です。求める2回目の時刻は4時38と2/11分です。
以上今回は時計算の基本を解説しました。時計算は答えが中途半端な分数になることが多く、そこがとっつきにくい点かもしれませんが、普通の速さの問題の距離の単位(km、mなど)が角度(°)に置きかえられただけで、時計算はれっきとした速さの文章題です。長針が短針より速く、両針は同じ方向に動くから、両針が動く分速の差5.5°がひんぱんに登場します。もし長針が止まっている短針を追いかけるなら速さは6°ですが、長針だけではなく短針の方も動いているから、速さの差の5.5°を長針が短針に追いつく速さと考えるわけですね。次回新作を書くときは、文字盤のない時計や、両針が線対称になる時刻など、もう少し突っ込んだ時計算の話を書こうと思ってます。
それでは今回の講座はここまでにしますね。次回からは2回連続で立方体の切断面の話です。なるべく早く出せるように頑張ります。また読みにいらしてくださいね。それじゃあまた~!(*^^)
みなさんへの宿題
時計の長針と短針が反対側に一直線(180°)になる時刻を2時台と10時台でそれぞれ求めてください。一直線になるのは2時台も10時台も1回ずつです。
解答したい方はページ下のコメントに書いてください。正解不正解をレスさせていただきます。お名前はニックネームでもかまいません。













