Newみんなの算数講座8 展開図から見つける高さ

今回は展開図を組み立ててできる立体の体積がテーマです。タイトルにも書きましたが、パッと見ただけではわかりにくい高さを、展開図の中から見つけることになります。
問題を出す前に、立体の重要公式を一つ確認しておきます。
角すいや円すいの体積=底面積×高さ×1/3
公式自体は知っている人も多かったと思いますが「×1/3」の理由はご存知でしょうか? 算数の範囲では説明がけっこう大変なのですが、一例を公式テクニック集に示してあります。理由が気になる方は下のリンクからご確認ください。
すいの体積の「×1/3」の理由
では今回の問題です。体積を求める問題なのですが、高さが見つけにくいせいか、意外と手こずる人が多いです。もちろん高さはわかるのですが、初めてこの問題を見た人にとっては、感動的な高さになるかもしれません。大げさかな(^^)/
下の図のように、1辺の長さが12cmの正方形の台紙から、底辺12cm、高さ3cmの合同な二等辺三角形を正方形の各辺に沿って4枚切り落とし、残った部分を組み立てて正四角すいを作ります。この正四角すいの体積を求めなさい。正四角すいの底面は正方形です。
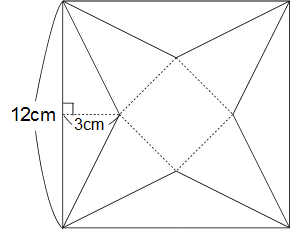
ではさっそく解説を始めます。
組み立てた正四角すいは下の図のようになります。高さのAOを赤い線、底面の正方形の対角線を点線で示しました。
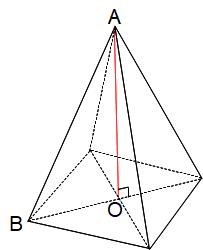
体積を求めるためには底面積と高さが必要です。まず底面積を求めましょう。
正四角すいの底面は正方形です。一辺の長さを求めることはできませんが、問題の展開図から対角線の長さが簡単に求められます。正方形の面積の公式は〈一辺×一辺〉ですが、それが使えないときはひし形の面積の公式〈対角線×対角線÷2〉を借りることができます。
正方形の対角線の長さは 12cmから3cmをふたつ引いて6cmだから、
底面積は6×6÷2=18cm²です。
メモ 正方形は、平行四辺形やひし形や台形が進化した四角形なので、面積の公式はどの四角形から借りてもかまいません。平行四辺形や台形の公式を借りることはありませんが、ひし形の公式はよく借りて使いますね。
次に四角すいの高さを考えましょう。
高さは上の図に赤い線で示した線分AOです。(Oは底面の正方形の中心)
ここが今回最大のポイントですが、四角すいの内部にある直角三角形ABOと合同な三角形が展開図の中にもあるのです。どこにあるかわかりますか?
じつは直角三角形ABOは、台紙から切り取った二等辺三角形をちょうど半分に切った形なのです。では、台紙から切り取った二等辺三角形の半分と、四角すいの内部の直角三角形ABOを比べてみましょう。
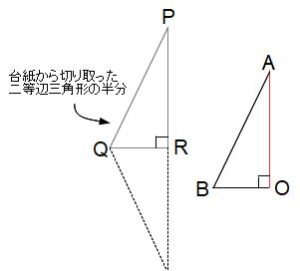
台紙から切り取った二等辺三角形の半分を△PQRとしました。
中学の図形で習う証明風に比べてみますね。
△PQRと△ABOにおいて、
PQ=AB(展開図を組み立てるとPQはABと同じ辺になる)
QR=BO=3cm
(QRは問題の条件より3cm、BOは正方形の対角線の半分だから3cm)
角PRQ=角AOB=90°
直角三角形の斜辺と他の一辺の長さが等しいから、
△PQR≡△ABO
二つの三角形が合同であることが確認できました。
さて、ということは?
そうそう、正四角すいの高さAOはPRと同じ長さだから台紙の一辺の長さのちょうど半分です。
AO=PR=12÷2=6cm →正四角すいの高さ
これで体積を求めるための底面積と高さがそろいました。
初めに確認したすいの体積の公式を使って、求める体積は、
18×6×1/3=36cm³です。
組み立てた正四角すいの内部にある直角三角形ABOが、台紙から切り取った二等辺三角形のちょうど半分になっている。これが高さを知るためのポイントでした。もちろんそうなるように出題者が数値を決めているのですが、言われてみないと自力では気づきにくいかもしれませんね。消化不良はよくありません。一度でわからなければ二度でも三度でも読み直してくださいね。
では今回はここまでにします。また次の講座で一緒に算数を楽しみましょう!
カーテンコール
途中、数学で習う証明風の書き方をしましたが、算数には証明という概念はありません。今回の問題でも、二つの三角形が合同とわかれば証明の記述は不要です。算数は間違いを直してあげることが先決だから、正しいことが正しい理由はあと回しにしても問題ないです。
みなさんへの宿題
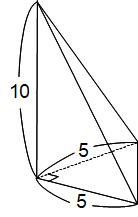 右の図のような高さが10cmの三角すいがあります。底面は等しい辺の長さが5cmの直角二等辺三角形です。この三角すいの表面積を求めてください。
右の図のような高さが10cmの三角すいがあります。底面は等しい辺の長さが5cmの直角二等辺三角形です。この三角すいの表面積を求めてください。
解答したい方はページ下のコメントに書いてください。正解不正解をレスさせていただきます。お名前はニックネームでもかまいません。













