NEWみんなの算数講座77 たとえば法で解く比の問題

こんにちは。ニューみん算講座77回目です。今回も僕の講座を通して、みなさんに役立つ算数を知っていただけたらと思います。
今回のテーマは比です。比は具体的な量ではありません。たとえば2:3という比は、10円と15円を表すこともあるし、60mと90mを表すこともあるし、400人と600人を表すこともあります。10:15も60:90も400:600も簡単に直せばすべて2:3ですね? こうした等しい比はいくらでも作れるから、だったら比の問題を解くとき、都合のよい形に直して使ってもかまわないはずです。比の自由度を活かし、比をうまく変えられるようになると、比の問題の対応力がだいぶ増しますね。
では具体的な問題を出して解説することにしましょう。
2つの容器A、Bがあり、容器Aにはアルコールと水が2:3の割合で溶けていて、容器Bにはアルコールと水が1:3の割合で溶けています。
アルコールと水を合計した重さは、容器Aが容器Bの2倍になっているそうです。では容器Aと容器Bの液体すべてをまぜたとき、溶けているアルコールと水の割合を比で答えてください。
この問題、与えられた比を別々にながめているだけではなかなか前に進まないと思います。僕なら問題に与えられた比の条件を整理したこんな表を書きます。
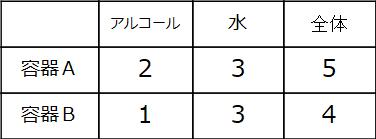
この表に変更を加えながら問題を解いていきますよ。
この表は、それぞれの容器内の横の関係は正しく示していますが、
「容器A全体の重さが容器B全体の重さの2倍」というタテの関係が表現されていません。全体のところを容器Aが容器Bの2倍になるように調整しなくてはなりませんね。
「容器Bが4だから、容器Aを8にすればいいですか?」←いきなり現れた生徒(*´з`)
それも間違いではないですが、容器A全体を8にすると、横の関係を維持するときに小数が現れてしまいますね。
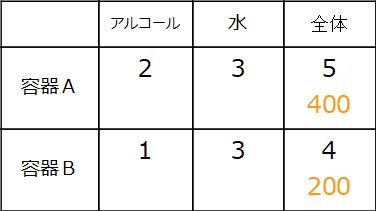
僕なら容器B全体を200にします。200という数字がどこからきたかはあとでわかります。容器B全体を200にすれば、容器A全体はその2倍で400になりますね?
表を更新しました。容器B全体を200、容器A全体を400にしてあります。変更した数はオレンジ色で示しました。
比は同じ数をかけても等しい比です。容器Aは5→400は80倍だから、アルコール(2)と水(3)も80倍し、
容器Bは4→200は50倍だから、アルコール(1)と水(3)も50倍します。
もう一度表を更新しました。
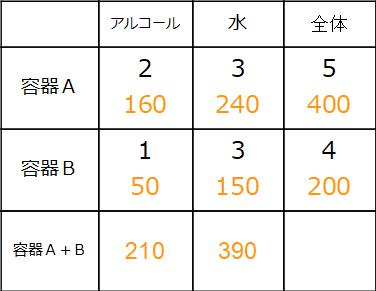
400と200を決めたあとは、比例配分でアルコールと水に分けてもよいです。
〈容器A〉
全体の重さ 400
アルコールと水の比 2:3
アルコール 400÷(2+3)×2=160
水 400-160=240g
*比例配分では、一方の量がわかったら、もう一方の量は引き算の方がラクです。
さてここまでくれば僕が容器B全体を200に決めた理由が見えてきたと思います。最初の全体の数が5と4でしょう? だから5と4のどちらでも割りきれる200が、この問題では都合のよい数ではないか?と予想したのです。
5と4の最小公倍数は20ですよね? 200ではなく20でもよかったと思いますが、食塩水の問題なんかでも20gより200gの方がありそうな数でしょう?自由に選べるので僕は200を選びました。
「容器B全体を100とかはどうですか?」
それでも大丈夫ですが、4→100は25倍だから、50倍より少し計算が面倒ですね。大差ないかな?100でもいいですね。
「そこまで予測して数を選ぶんですか?」
こうした作業に慣れてくると、その後の処理がラクな数が浮かぶようになります。
さて解答まであと一歩です。
容器Aと容器Bのアルコールと水をそれぞれ合計すると、
アルコール 160+50=210
水 240+150=390
よって求める解答は210:390
この比は30で割って簡単な比にすることができます。
210:390→7:13 (答え)
比を自由度をうまく利用することによって、それほど苦労せずに答えを出すことができました。
***
今回の解き方はいかがでしたか? 要点をまとめておくと、いくつかの比があったとき、横の関係とタテの関係が崩れないなら、解答者が扱いやすい数に直して考えてよいということです。
最後になってしまいましたがタイトルの話。僕は授業でこうした解き方を「たとえば法」と呼んでいます。たとえばの数で考えるという意味ですね。算数に慣れてる人には当たり前のことでしょうけど、慣れていない人は発想しにくい方法みたいです。自分で数を決めちゃうというところが反則っぽく感じるのでしょうかね。でもこうした自由さが比の持ち味なんです。いつか皆さんの前に「たとえば法」が使える問題が出てきて、皆さんが「たとえば法」でやっつけることを期待しています。
では今回はこれでおしまい。また次の講座の発表を楽しみにしていてくださいね。














