NEWみんなの算数講座95 互いに素という条件

みなさんこんにちは。ニューみん算講座95回です。５の倍数回に達したので、お宝ファイルが１冊子増えて全19冊子になります。（お宝ファイルについては講座の最後をご覧ください）

今回の講座では、整数問題のよくできた良問を題材にして、約数、公約数周辺のお話をしようと思います。互いに素（たがいに・そ）という言葉が出てきますよ。みなさんもぜひいっしょに頭を動かし、整数の世界に浸ってみてください。
ではさっそく問題です。

すごくシンプルな問題文ですね。パッと見た感じはそんなに難しそうな気はしません。ところがこれがなかなか対処に困る問題なんですよ。問題がシンプルすぎて、どこに糸口を見つけたらよいのか悩んでしまう感じでしょうか。

では解説を始めますので、がんばってついてきてください。整数Ａに当てはまる整数はけっこうたくさんありますよ。

まず、次の性質が頭にないと解説の路線に乗れません。

公約数は、最大公約数の約数！

簡単な例として20と30で考えてみます。
20と30の最大公約数は10ですね？
そして10の約数は１、２、５、10です。この１、２、５、10が過不足なく20と30の公約数です。公約数というと、つい最大公約数だけに目がいきがちですが（すだれ算の計算が有名だからでしょう）、最大公約数というのは公約数のなかで一番大きいものであり、ふつうに公約数といえば最大公約数以外の公約数もあります(たとえば１は必ず公約数)。上の１行はしっかり抑えてください。

公約数が最大公約数の約数ということから、問題の条件を次のようにとらえることができます。

Ａと42に公約数が４つある
➡Ａと42の最大公約数が約数を４つ持つ整数

大丈夫ですね？Ａと42の最大公約数をＰとすると、Ｐの約数が４つあるから、Ａと42の公約数が４つということです。

次にポイントになるのは、ここが単純なことで意外と盲点になってしまうようですが、

Ａと42の最大公約数Ｐは42の約数の中に含まれています。

Ａと42の最大公約数とは「Ａと42に共通する約数の中で一番大きいもの」だから、Ａと42の最大公約数が42の約数に含まれているのは当たり前ですね。

話を進めます。
「Ａと42の最大公約数Ｐ」の候補になる42の約数は次のとおりです。

Ａと42の最大公約数Ｐの候補（＝42の約数）
１、２、３、６、７、14、21、42

Ｐは約数を４つ持つ整数だから、この候補の中から約数を４つ持つ整数を探します。該当するのは６と14と21です。

６の約数（４つ）１、２、３、６
14の約数（４つ）１、２、７、14
21の約数（４つ）１、３、７、21
＊１の約数は１だけ。２、３、７は素数だから約数は２つ。42には８つの約数があります。
＊約数の個数の数え方については本講座最長老の１回目の講座もご覧ください。

あとひと踏ん張りです。Ａと42の最大公約数Ｐは６、14、21のどれかです。
その３つの場合に分けて、すだれ算をイメージしながらＡを調べます。

●Ｐ＝６のとき

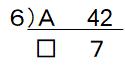
最大公約数のＰが６だから、Ａと42は６で割り切れます。
このとき、□と７は互いに素といって、１以外に公約数を持たない関係でなくてはなりません。つまり、６で割れたあとに他の整数で割れることはないということです。もし６に続いて他の整数で割れたら、最大公約数が６ではなくなってしまうからです。
＊算数界の専門用語コーナーにも「互いに素」の説明があります。

７は素数だから、□が７の倍数でなければ互いに素の条件はクリアします。
すだれ算の計算方法より、　Ａ÷６＝□ 　➡　 □×６＝Ａ　です。
Ａが２ケタという問題の条件を考えると、
□に入る整数は２、３、４、５、６、８、９、10、11、12、13、15、16の13個です。
＊□＝１はＡが２ケタにならない。
＊□＝７、14は「□と７が互いに素」に反します。
＊□＝17以上はＡが２ケタに収まりません。

問題で求めるのは個数ですが、整数Ａを列挙すると、
12、18、24、30、36、48、54、60、66、72、78、84、90です。（13個）

●Ｐ＝14のとき

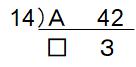
Ｐ＝６のときと同じように考えます。□と３が互いに素であること、□×14で求めるＡが２ケタであることに注意すると、
□に入る整数は１、２、４、５、７の５個です。
＊□＝３、６は「□と３が互いに素」に反します。
＊□＝８以上はＡが２ケタに収まりません。

整数Ａは14、28、56、70、98です。（５個）

●Ｐ＝21のとき

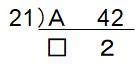
考え方は同様です。□と２が互いに素であること、□×21で求めるＡが２ケタであることに注意します。
□に入る整数は１と３の２個です。
＊□が偶数のとき、「□と２が互いに素」に反します。
＊□＝５以上はＡが２ケタに収まりません。

整数Ａは21、63です。（２個）

お疲れさまでした。以上ですべてのＡを求めることができました。考えられるＡは全部で13＋５＋２＝20個あります。

＊＊＊
いかがでしたか？すだれ算は、最初に並べて書く２数がわかっていれば簡単なのですが、どちらかが（両方が）わからないときは、逆からたどって調べますので「互いに素」の制約を気にしなくてはなりません。慣れていないとウッカリするところかもしれません。今一度、最大公約数を求めるすだれ算について、計算方法の確認をしてくださいね。
【最大公約数のすだれ算➡最初に並べた数をすべて割れる数で割り、割れる数がなくなったら、割った数全部をかけ算して求めます】

今回「約数が４つ」というキーワードがありましたから、近々、約数の個数別に整数を分類するという講座も書きたいと思います。100回目の記念講座をそれにしましょうかね。
それでは今回の講座はここまでにします。また次回の講座でいっしょに算数を勉強しましょう。

インフォメーションボード

〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。

〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。

〈算数講座へのご意見や質問／ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。

〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、５講座ずつを１冊子にまとめ、「なかとじ印刷」した片側Ａ５サイズ（開くとＡ４）のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら