Newみんなの算数講座66 切り口のレジュメ(後編)

今回の講座66は前回の前編に続いて立方体の切り口について解説します。まだ前編を読んでない方は、先に一つ前の講座65を読んでくださいね。
前編では、立方体を切断する問題が辺上に3点を与える理由、そのうちの2点をつなぐことができる場合とできない場合、平行な面に平行な線を引く手順などを解説しました。3つのレジュメと1つの反則がありましたね。前編はそこまでの知識で対処できる問題でしたが、今回はそれだけでは不十分なパターンです。ではそのパターンの問題を出しますね。
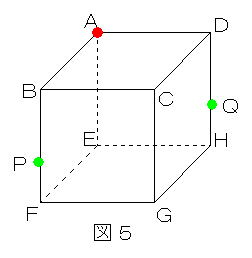
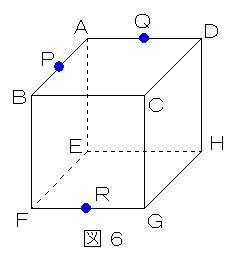
下の図5・図6について、与えられた3点をすべて含む平面で切断したとき、切り口はどのような図形になりますか? もっともふさわしい図形の名前を答えてください。カラー表示の赤い点は立方体の頂点、青い点は立方体の各辺の中点、緑色の点は立方体の各辺の3等分点(下寄り)を表しています。
立方体切断のレジュメと反則 (追加版)
レジュメ1
立方体の同じ面上にある2点は直接つなぐことができます
*同じ面上というのは立方体の6つのどの面上でもかまいません
反則!
立方体の同じ面上にない2点を直接つなぐことはできません
レジュメ2
平行に向き合っている面では切り口の辺も平行に向き合います
*平行な面に切り口の辺が存在するなら…です
レジュメ3
切り口の名前は、文科省の検定教科書に出てくるもっともふさわしい図形の名前を答えます
*平行四辺形を四角形、二等辺三角形を三角形などは不正解です
レジュメ4
平行な面に現れる相似な三角形に注目すると、切り口の辺の通過位置を知る手がかりになります
*切断後の立体の求積問題ではとても重要です
レジュメ5
与えられた図の中だけで切り口の作図ができないときは、立方体の辺を延長し(立方体の面を広げ)、切り口の図形を大きく捉えるようにします
図5解説
まずAとP、AとQをつなぎます(レジュメ1)。PとQはつなげないので、右側の正方形にAPの平行線QSを、手前の正方形にAQの平行線PRを引きます(レジュメ2)。RとSは同じ面上の点なのでつなぐことができます。
図5の切り口はAP=AQ、PR=QSで、さらにAPとQS、AQとPRが平行になっている左右対称な貝殻のような形をした五角形です。
*特長のある五角形ですが特別な名前はないので、単に五角形と答えて大丈夫です。
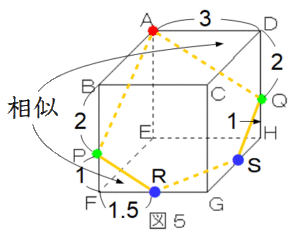
くわしく
レジュメ4に書いたように、相似な三角形の辺の比から、RとSが辺の中点であることが確認できます。
正方形の1辺の長さを3とすると、P、Qは辺の下寄りの3等分点だからBP=DQ=2、PF=QH=1です。
PRとAQは平行だから△RFPと△ADQは相似な三角形で、
FP:DQ=RF:AD
わかっている数値をあてはめて 1:2=RF:3
比例式は内項と外項の積が等しいから 2×RF=3
よってRF=3÷2=1.5
この長さは正方形の1辺の長さの半分だから、RがFGの中点であることがわかります。このような計算は、切断後の立体の求積問題でとても重要な手がかりになります。
*SがGHの中点であることも△SHQと△ABPの相似から同様にわかります。
図6解説
この切り口の作図にはレジュメ5の方針が必要です。辺を延ばし、面を広げることで切断を大きく捉えるようにするのです。与えられた3点はP、Q、Rでした。PとQをつないだあとは次のような方針で考えます。
PQを両側に延長し、CBの延長との交点をX、CDの延長との交点をYとします。(延長した線は水色で表示しました)
このように延長するとXとRは同じ面上の点となり、つなぐことができます。XとRをつなぐ直線は、BFの中点Uを通り、CGの延長上のZに到達します。ここで切り口の面がU、Rを通ることがわかりました。
*切り口の通過点が立方体の各辺の中点になることは、各所にある三角形(△APQ、△BPXなど)がどれも合同な直角二等辺三角形であることから確認できます。
次に平行になっている正方形に注目し、Rを通るPQの平行線RT、続いてTを通るPUの平行線TSを引きます。ここまでくればSとQは同じ面上にあるからつなげます。図6の切り口は、立方体の内側をひと回りするような、すべての辺の長さが等しい正六角形です。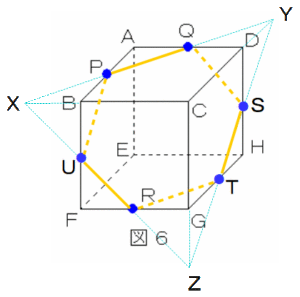
くわしく
立方体を対角線AC(面AEGC)を境にして見ると、頂点Bの周辺と頂点Dの周辺が左右対称の作図になっていることが確認できると思います。対角線CF(面CDEF)を境に見れば、頂点Bの周辺と頂点Gの周辺が左右対称です。
また、この正六角形の切り口は、立方体を2つのまったく合同な立体に切り分けています。切り口の正六角形の前後にある立体は天地が逆になった同じ立体です。
切り口講座の後編、理解していただけたでしょうか? 前編よりもやっかいな作図でしたが、貝殻型の五角形も正六角形もとてもきれいな切り口ですよね。最後に立方体の切り口としてよく出る図形を並べておきましょう。どのような3点が与えられればこのような切り口になるか? 逆に考えてみるのも勉強になると思います。
よく出る立方体の切り口の図形
三角形……二等辺三角形、正三角形
四角形……正方形、長方形、平行四辺形、ひし形、台形(等脚台形)
多角形……貝殻型五角形、正六角形
*これ以外にも一般の三角形~六角形は切り口として考えられます。できそうで無理なのが直角三角形と正五角形。また七角形以上の多角形はあり得ないです。
立方体の切り口問題はけっこう出題されますからね。いろいろな3点の与えられ方に対応できるようにしてください。さらに発展させると、切断後に二つに分かれた立体について体積や表面積を考える問題がありますね。それについては新作予定表に組み込みましたからそのうち書いて発表したいと思います。
ではでは2回連続の切り口講座をこれで終わります。次回は少し前にもあったけど、元祖講座を不採用にして新作のNo.8です。百五減算(ひゃくごげんざん)というスペシャルな整数問題を出す予定です。大変な内容だから少し時間かかるかな。どうぞお楽しみに~(^^)/
みなさんへの宿題
下に示した立方体の切り口(台形)の4辺をその下の展開図に正しく記入してください。
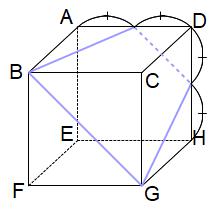
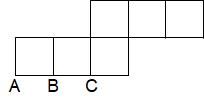
これはコメントフォームには解答できませんね。何かコメントをくださればメールでお返事しますから、解答はそのメールに写真などでお送りください。正解不正解をお知らせさせていただきます。お名前はニックネームでもかまいません。
-
前の記事

Newみんなの算数講座65 切り口のレジュメ(前編)
-
次の記事

Newみんなの算数講座67 百五減算











