Newみんなの算数講座50 ザ・Ｎ進法(前編)

ニューみん算講座。ついに節目の50回目を迎えました。記念の50回目のためにとても面白い内容を使わないでとってありました。今回と次回は２回連続でＮ進法の講座です。われわれがいつの間にか洗脳されてしまっている数の常識に、たまにはさからってみない？という話です。ぜひいつもとちがう数の仕組みを楽しみながら算数の知識を増やしてくださいね。

洗脳なんて言葉を使ってしまいました。洗脳は言い過ぎだとしても、Ｎ進法を考えるときの敵は数の仕組みに対する思い込みかな。われわれは小さい頃から数は10ずつ束(たば)にするものだと思い込んでますよね。そしてその前提で10進法という数の仕組みを毎日当たり前のように使ってます。
１、２、３、４、５、６、７、８、９
ここまでがひとけたの数で、この次が10です。つまり一の位は９がマックスで、その次は一の位を０にクリアーし、クリアー１回の履歴として十の位を１にします。99まで進むと十の位もマックスだから、十の位も一の位もクリアーして百の位を１にします。99の次は100ですね。この仕組みが10を束と考える10進法ですね。

もちろん日常生活では10進法に何の問題もありません。10進法は日本に限らず世界の常識ですから。身のまわりで純粋な10進法といえないのは時間ぐらいかな。９時59分から５分たつと10時４分。60以上の整数を使わない時間の表し方は普通の10進法とはちょっと違いますね。それでも時間を読むときは、にじゅうさん分(23分)のように10進法と同じように読むから、それほどの違和感は感じないでしょう。

が、しかし！

算数や数学の世界には、もっともっと明確に10を１つの束としない考え方が存在します。これから説明するＮ進法には10を束とするという固定観念は一切ありません。ときには２が束だし、ときには５が束です。束が８ずつのときも12ずつのときもあります。読み方も10進法とは違いますね。10進法以外の数は、たとえば125なら「いちにーご」のように棒読みすることになってます。日常生活で使うことはないと思いますが、算数や数学のテストにはとてもよく出題されます。テストに限らず、頭の体操にはもってこいのユニークな考え方ですよ。

では、Ｎ進法の例として２進法、５進法、８進法、12進法を解説することにします。数字は０から９まであって、数は10ずつ束にするという常識にはこだわらないでくださいね。

では次に、こうしたＮ進法で表された数が普通の10進法のいくつにあたるのか？という変換について、具体的な問題を使って説明します。算数ではここが一番大事なところです！
＊逆の変換10進法→Ｎ進法は次回の後編で扱います

Ｎ進法の数を10進法の数に変換するときは、各位の数字と各位の位取りをかけ算したものをすべて合計します。

では設問について10進法に変換していきます。各位の数字と位取りを対応させた図を作ってみました。左から上位の位です。
(1)

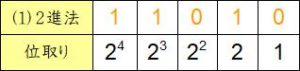
各位の数字を位取りとかけ算して合計します。
２⁴×１＋２³×１＋２×１＝16×１＋８×１＋２×１＝16＋８＋２＝26
数字が０の位はスルーしてよいです。２進法の場合、０以外の数字は１しかないから、１倍も省いて16＋８＋２のように位取りをたし算して大丈夫です。

(2)

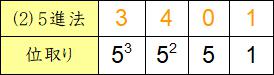
各位の数字を位取りとかけ算して合計します。
５³×３＋５²×４＋１×１＝125×３＋25×４＋１×１＝375＋100＋１＝476

(3)

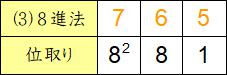
(1)(2)と同様です。
８²×７＋８×６＋１×５＝64×７＋８×６＋１×５＝448＋48＋５＝501

(4)

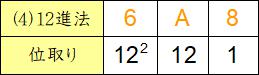
12進法には９より大きいひとけたの数字Ａ、Ｂがあり、10進法への変換ではＡを10、Ｂを11と考えます。
12²×６＋12×Ａ＋１×８＝144×６＋12×10＋１×８＝864＋120＋８＝992

数字は０から９という常識をくつがえしたＮ進法。ここまでどうですか？ たまにはふだんの発想を捨てた数の世界に身を置くのも楽しいことですね。ようは数字が10個あるから10進法が成り立つわけで、数字を減らしたり増やしたりすることで、10進法以外の数の表し方も生まれるわけです。算数の問題でよく見かけるのは２進法～５進法と８進法かな。Ｎが10を超えるＮ進法は算数ではレアだと思いますが、コンピューターの内部記憶などでは16進法が使われたりしてますね。パソコンをよく使う人なら、なにかのときに5AE0のような数字と英字が混ざった表示を見たことありませんか？ あれが16進法ですね。16進法は９のあとにＡ～Ｆの英字を追加して使い、４ケタの最大数はFFFFです。これは10進法の65535を表してますよ。同じケタ数で10進法の６倍以上の事柄が記憶できるということですね。

Ｎ進法の知識は算数のみならず、中学や高校の数学、就職試験などでも活きてくるでしょう。もしＮ進法を忘れたら、またこのページを読みにきてくださいね。ずっとここに置いてありますから;^^)
では次回の後編でもう一回Ｎ進法講座を続けます。今回と逆に10進法の数をＮ進数の数に変換する方法を中心に取り上げたいと思います。それじゃあ次の後編でまたお目にかかりましょう。さよなら～！