NEWみんなの算数講座98 内部底辺

みなさんこんにちは。NEWみんなの算数講座98回目です。前回の最後で出した覆面算の解説は本題のあとで書きますね。
今回の本題は、平面図形のジャンルから、三角形をテーマに取り上げます。三角形の面積を求めるとき、底辺といえば、3つの辺のどれかと思うかもしれませんが、じつは三角形の底辺は3つの辺のどれかとは限らないです。この発想が、三角形の面積を求める問題で役に立つことがあります。
それではタイトルの内部底辺が、いったい何を意味しているのか?次の問題を使って解説したいと思います。
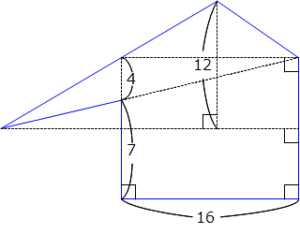 左の図で、青い線で囲まれた図形の面積を求めてください。(単位 cm)
左の図で、青い線で囲まれた図形の面積を求めてください。(単位 cm)
この図形の面積を、1つの式でいっぺんに求めることができないのはおわかりでしょう。
だから当然分割して考えますね?しかし、おかしな分割をしてしまうと、迷路をうろうろする羽目になってしまいます。たとえばタテ11cm、ヨコ16cmの長方形の面積を求めてしまうと、残り2ヶ所の三角形の面積を求めることができません。
では他にどのような分割が考えられるでしょうか?
分割案はそれほどたくさんあるわけではないので、「下にある台形と、その上にある三角形に分ける」と考えた人がいると思います。
その分割で正解です。
では台形の方を解決させてしまいましょう。
下にある台形は〈上底7cm、下底4+7=11cm、高さ16cm〉を使って、普通に台形の公式で計算します。
(7+4)×16÷2=88cm2 …下にある台形の面積(ア)
台形は簡単に解決ですが、その上に乗っかっている三角形の面積をみなさんは求めることができますか?
三角形の面積といえば、普通は3つある辺のどれかを底辺に選びます。しかし次の図を見てください。面積を求めたい三角形をオレンジ色で囲んでみましたが、3つの辺のどこにも長さは示されていません。しかも、これらの3つの辺の長さを求めるのは、数学を持ち出せばなんとかなりますが、算数では無理です。
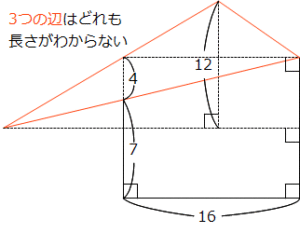
ではどうするか?
じつはこのオレンジで囲んだ三角形、3つの辺のどれかが底辺という発想さえ捨てれば、きれいに面積が求められるのです。この講座のタイトルを思い出してください。そう、内部底辺です。もう一つ図を作りましたのでご覧ください。
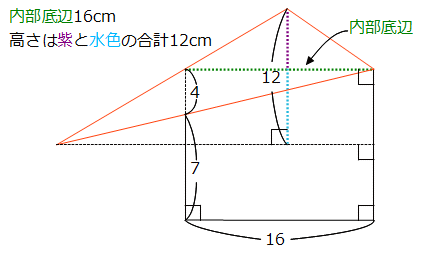
このオレンジの三角形の底辺を、三角形の内部に引かれている緑色の点線と見るのです。内部にある底辺だから内部底辺です。
*僕のネーミングで、正式な言葉ではないです。だけどわかりやすいでしょう?生徒にもとても評判がいいネーミングです。
すると、その内部底辺を境にして、オレンジの三角形を上下2つに分ければ、上の三角形の高さは紫の点線、下の三角形の高さは水色の点線です。
紫と水色のそれぞれの長さはわかりませんが、合計すると12cmとわかっています。上下どちらも底辺が16cmなので、高さは紫と水色をまとめて12cmで大丈夫です。
ではオレンジの三角形の面積を求めます。〈内部底辺16cm、高さは合計で12cm〉です。
16×12÷2=96cm2 …台形の上に乗っているオレンジの三角形の面積(イ)
これで問題は最後まで解決しました。(ア)と(イ)を合計して、今回の問題の解答は、88+96=184cm2です。
***
いかがでしたか?三角形の底辺を内部に考えるという発想の切り替え方を覚えておいてくださいね。
さて今回は長くなりますが、ここから前回の覆面算の解説をします。
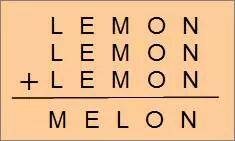
まず、一の位と十の位を考えてみます。
N+N+NやO+O+Oの答えの一の位がNやOになるのは、次のどちらかしかありません。
0+0+0=0 5+5+5=15
N+N+Nが5+5+5の場合、十の位に繰り上がりの「1」が発生します。繰り上がりの「1」を入れてO+O+Oの一の位をOにすることはできないから、N=0、O=5とわかります。一の位は0+0+0=0、十の位は5+5+5=15で、百の位に繰り上がりの「1」が発生します。
次に一万の位に注目します。5ケタの整数を3つ加えた合計が5ケタに収まるのは、一万の位の数字Lが3以下の場合です。4万以上の整数を3つ加えたら、それらの合計は6ケタになってしまいます。Lの候補は1か2か3です。
*LはLEMONの一万の位と、たし算の答えMELONの百の位で使われています。
ではLを1、2、3に分けて、LEMONの百の位Mを調べてみます。
[L=1]百の位M+M+Mに十の位からの繰り上がり「1」をたしてLを1にすることはできません。以下の式で確認してください。1+1+1+1=4、2+2+2+1=7、3+3+3+1=10
4+4+4+1=13、6+6+6+1=19、7+7+7+1=22
8+8+8+1=25、9+9+9+1=28 [L=2]百の位M+M+Mに十の位からの繰り上がり「1」をたしてLが2になるのは、Mが7のとき(7+7+7+1=22)です。…ア
[L=3]百の位M+M+Mに十の位からの繰り上がり「1」をたしてLが3になるのは、Mが4のとき(4+4+4+1=13)です。…イ
この時点でLとMの組み合わせが
(L=2、M=7)…ア
(L=3、M=4)…イ
にしぼられましたが、じつはイの場合はありえません。理由は千の位との関係です。イの場合、百の位からの繰り上がりが「1」になりますが、その繰り上がりをたして、千の位E+E+Eの一の位をEにすることはできないのです。
L=2、M=7が決定します。
残りのEは4です。千の位で百の位からの繰り上がり「2」もたして計算すると、4+4+4+2=14となり、さらに一万の位も2+2+2+1=7となってすべての辻つまが合います。
*Eを9と考え、千の位を9+9+9+2=29とすると、ここまではうまくいきますが、一万の位に繰り上がり「2」が発生してしまい、一万の位で辻つまが合わなくなります。
では解答を整理します。3つあるLEMONは24750
MELONは24750+24750+24750=74250です。正解だった人、どれくらいいたかなあ?
***
長くなりました。今回の講座98回はこれで終わりにします。次回の99回でまたいっしょに算数を勉強しましょう。それではまた~!
インフォメーションボード
〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。
〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。
〈算数講座へのご意見や質問/ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。
〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、5講座ずつを1冊子にまとめ、「なかとじ印刷」した片側A5サイズ(開くとA4)のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら













