NEWみんなの算数講座86 三角形を全部見てはいけない

みなさんこんにちは。ニューみん算講座86回目です。
今回は久々に図形を取り上げようと思います。だいぶ前に第４回でメネラウスの定理を書きましたが、今回はそのご友人のチェバの定理が関係しています。
図形の中では少し応用的な話ですが、特別難しいということはないと思います。がんばってついてきてくださいね。

何も予備知識を持たずに考えるのはキツいと思うので、少々基本にかえって説明をします。
次の図を見てください。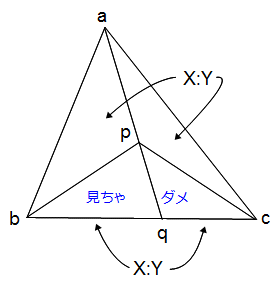

この図を見たときに、底辺bqとqcの比がX:Yだから、三角形abqと三角形aqcや、三角形pbqと三角形pqcの面積の比がX:Yになることはおわかりになる人が多いと思います。
はいそうです。高さの等しい三角形は〈底辺の比〉＝〈面積の比〉ですね。

おわかりになる人が少ないと思うのは、
三角形abpと三角形apc、そう、図をX:Yの底辺方向から見たとき、上に浮いている感じになっている２つの三角形ですも面積の比がX:Yになるのです。

図には見ちゃダメと入れてみました。見ちゃダメのところを見ずに、上に浮いている三角形abpと三角形apcの面積の比がX:Yと判断できるようになれば、この講座を続けて読んでいただいて大丈夫です。

理由は16回目の講座で紹介した加比の理の考え方です。面積比がX:Yになっている図形に対して、同じく面積比がX:Yになっている図形をくっつけたり引いたりしても、その和や差ではX:Yの面積比が維持（いじ）されるのです。
三角形abq：三角形aqc＝X:Y
三角形pbq：三角形pqc＝X:Y
だから引き算した三角形abp：三角形apcもX:Y
いまいち不安な人は16回目の講座も目を通してみてください。

では問題の解説に。
いまの浮いている三角形の話が理解できると、おもしろく解けてしまうと思います。もう一回問題図を貼りましょう。

まず、この図を真下の方向から見てください。
浮いている三角形ＡＢＯとＡＯＣの面積の比が５：３になりますね？
そして次に左の方向から見てください。辺ＡＢが下になるように図を回してくれてもよいと思います。あ、それは印刷している人しかできないですね。だったら自分の顔を辺ＡＢが下になる位置に動かしてみてもよいでしょう。パソコンの画面を左側からのぞき込む感じでしょうか。
ＡＵ：ＵＢ＝４：７だから、浮いている三角形ＡＯＣとＯＢＣの面積の比が４：７になりますね。ではいまわかった５：３と４：７を書き込んだ図を用意します。

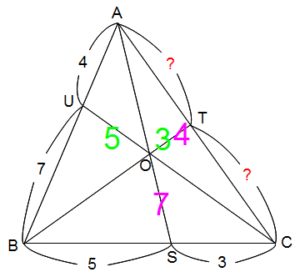
２種類の比を黄緑と紫（むらさき）で色分けしました。インターネットはカラーが使えるから説明がラクです。ふつうの授業だったら数字を○や□で囲んで表現するところです。
説明はもう少し続きます。
同じ三角形が３と４になっているでしょう？このようなとき、算数では比をそろえるといって、３と４を最小公倍数の12にそろえるのです。３が12になるから黄緑の比は４倍、４が12になるから紫の比は３倍します。すると次の図のようになります。

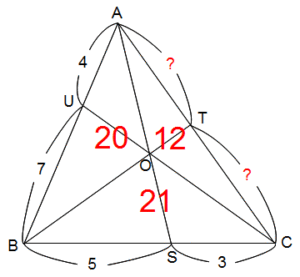
黄緑と紫をそろえた新しい比を今度は赤で示しました。そうそう、これでもう答えが出てしまってますよ。
問題で求めるＡＴ：ＴＣは、図を右の方向から見て、さきほどの浮いている三角形の法則をもう一度使えば、三角形ＡＢＯとＯＢＣの面積の比と同じでしょう？
問題の解答は20：21です。

＊＊＊
いかがでしたか？
とても楽しい考え方ですよね。知らなかった人にとっては感動モノだったかもしれません。この講座を読んでよかった？
うれしいなあ。どうもありがとうございます(^.^)
お世辞でもほめられると調子に乗っちゃう人なんで、お礼にもう一つプレゼントしちゃいましょう。

じつは算数では習わないことが多いはずですが、数学で習うチェバの定理という有名な定理によれば、
今回の問題図について

が成り立ちます。

左側の分数から〈分母 分子 分母 分子 分母 分子〉の順に、頂点Ａからスタートした線分が、ＡＵ→ＵＢ→ＢＳ→ＳＣ→ＣＴ→ＴＡのようにグルッと一周してＡに戻っています。とても覚えやすい定理ですよね。
公式の理由ですか？
上の分数をさっき説明した「浮いている三角形の面積」で置きかえてみてください。
たとえば「AUぶんのUB」は「三角形AOCぶんの三角形OBC」のように。すると分母と分子がきれいに約分されて何も残らずに１になるはずです。
冒頭にも書きましたが、第４回で説明したメネラウスの定理と、今回のチェバの定理は、中学高校の数学で兄弟のようにセットで出てくる定理です。記憶力に自信がある人は覚えておくと有利でしょう。

では今回の講座はここまでにしますね。次回87回も楽しみに待っていてください。それでは～。

カーテンコール
メネラウスもチェバも覚えることが必須ではありません。なぜなら定理を忘れていても、上で解説したように考えれば答えが出せるからです。もちろん覚えていることが損にはならないですけどね。記憶力に自信がある人は覚えていただき、そうでない人はふつうに解けることを目指してください。

インフォメーションボード

〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。

〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。

〈算数講座へのご意見や質問／ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。

〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、５講座ずつを１冊子にまとめ、「なかとじ印刷」した片側Ａ５サイズ（開くとＡ４）のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら