NEWみんなの算数講座85 あまりが等しくなる線分図

みなさんこんにちは。
今回は、とてもよく出る割り算とあまりの問題を解説します。いくつかの整数を同じ整数で割ったとき、あまりが等しくなるという条件から、割った整数（割る数）を求める問題です。解いていく途中で、その整数が条件を満たすかどうかのチェックが必要で、そのチェックを怠（おこた）ると、余計なものまで答えてしまうことになります。出題されることがとても多い問題なので、よく読んでしっかり理解してくださいね。

正直に式を作ってみると次のようになりますが、わからないところが多すぎて、式だけで何かをつかむのは難しいです。

128÷□＝〇あまり△
200÷□＝●あまり△
236÷□＝◎あまり△

求めたいのは□ですが、それ以外にもわからないところだらけですよね？

それをどうするか？
この問題は数式の問題なのに、意外にも線分図を書いてみるのが名案なのです。さっそく線分図を作りました。

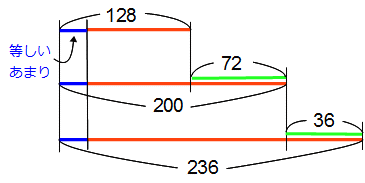
線分図はこのようになります。
まず、割ったときに等しくなるあまり（△）を線分図の左側でそろえます。青い線のところです。

すると残ったオレンジの線のところ（３本とも）は、あまりがなくなったわけだから□で割ると割り切れることになりますね。
しかし残念ながらオレンジの線の長さを求めることはまだできないです。

そこで注目するのが緑の線です。オレンジの線がどれも□で割り切れるなら、オレンジの線とオレンジの線の差も□で割り切れるはずですよね？
＊たとえば16も48も８で割り切れます。その差の32（＝48－16）も８で割り切れます。

オレンジの線とちがい、緑の線の長さは簡単に計算することができます。緑の線の長さは
200－128＝72と、236－200＝36です。

ポイントを整理します。
問題で求めたい整数の□は、緑の線の72と36を両方とも割り切れる数です。つまり72と36の公約数ですね。

公約数とは最大公約数の約数すべてです。
72と36の最大公約数は36だから、割る数の□として考えられる整数は、
１、２、３、４、６、９、12、18、36 （36の約数）です。

８個の整数が候補になりましたが、これらがすべて答えになるわけではありません。
なぜか？
それは128や200や236を割ったときに、割り切れてしまう整数を除外しなくてはならないからです。割り切れてしまったら余りが出ませんよね？

ではていねいにそのチェックをしてみましょう。
まず１と２は落選です。128÷１、128÷２　どちらも割り切れてしまいます。３つの整数のうち、一つでも割り切れたら落選だから、他を割るまでもないでしょう。（200も236も１と２では割り切れます）

３はセーフみたいですね。128、200、236のなかに３で割り切れる数はないです。すると６、９、12、18、36がまとめてセーフであることもわかります。なぜなら６、９、12、18、36はどれも３の倍数だから、３で割り切れなかった数が６、９、12、18、36で割り切れるはずがないからです。

あとは４が残ってますね。４は残念ながら落選です。128÷４が割り切れてしまうのですね。（200÷４　236÷４も割り切れます）

これで無事に最終チェックが終了しました。この問題の解答として残る整数は
３、６、９、12、18、36です。

□＝３で確かめをしてみましょうか。
128÷３＝42あまり２
200÷３＝66あまり２
236÷３＝78あまり２
確かにあまりがすべて等しくなりますね。３以外についてはみなさんでたしかめてみてください。

＊＊＊
線分図から手がかりを得るわり算とあまりの問題、いかがでしたでしょうか？
式を作るだけでは解き方が見えにくい問題なのですが、線分図を書いてみることで理解がしやすくなりました。この問題を中高生に出すと、文字を４つも５つも持ち出して数式だけで解こうとしますよ？それでもなんとかなるのですが、これは算数の知恵の方が上を行っている気がしますね。この問題がテストに出たら、ぜひ線分図といっしょに攻略したことを思い出してくださいね。

ではまた次の講座で楽しい算数のお話をしたいと思います。今回はこれでさようなら！

カーテンコール
最後に除外した１、２、４も「あまりが０」と考えれば問題の条件からはずれているわけではありません。しかし常識的に考えて、あまりが０のとき（割り切れたとき）に、あまりが等しくなったとは言わないでしょう？テストに出題される場合も、１、２、４を入れたら不正解になるでしょうね。

インフォメーションボード

〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。

〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。

〈算数講座へのご意見や質問／ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。

〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、５講座ずつを１冊子にまとめ、「なかとじ印刷」した片側Ａ５サイズ（開くとＡ４）のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら