Newみんなの算数講座19 面積図で解く？比で解く？

今回の速さの問題には甲乙つけがたい２つの有力な解き方があります。むかしホームページでアンケートをとったことがありますが、ほとんど真っ二つの結果でしたね。みなさんはどちらが頭になじむでしょうか？僕の意見は最後に書きますね。

２つの有力な解き方がある速さの問題。それはこんな問題です。

では有力な２つの解き方を順番に紹介します。

解き方１　面積図を使って解く
次のような面積図を書いて考えます。面積図とは、２つの量の積を面積によって表現する算数ツールです。〈タテ〉×〈横〉が長方形の面積になるのと同じように、速さの問題なら〈速さ〉と〈時間〉をかけた〈距離〉が面積になります。

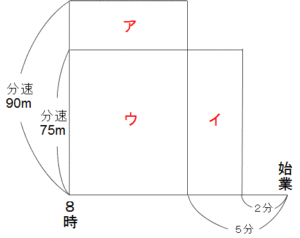
面積図のタテが速さ、横が時間の経過です。
「分速90ｍで行くと 始業５分前に着く」
「分速75ｍで行くと 始業２分前に着く」
この２つの条件を、長方形を重ねて書くことで表現します。
学校までの距離は変わらないから、重なっている２つの長方形の面積は等しく、共通部分のウを取り去ることで、アの面積とイの面積が等しいことがわかります。

イの面積＝75×(５－２)＝225　→アの面積も225
アの横の長さ　225÷(90－75)＝15
よって、分速90ｍで行くと15分かかることがわかり、始業時刻は ８時＋15分＋５分＝８時20分
家から学校までの距離は 90(m／分)×15分＝1350ｍ
無事に解答が求められました。

解き方２　比を使って解く
比が使える生徒ならこちらの解法もかなり有力です。

家から学校までの距離は変わらないので、２つの行き方で、速さの比と時間の比が逆の比になります。

重要メモ　距離が一定のとき、速さの比と時間の比は逆の比になる

分速90ｍで行く場合と分速75ｍで行く場合の速さの比は
90：75＝６：５
所要時間の比は逆の比になって５：６です。解説の都合で〇で囲んで⑤：⑥と直しますね。
所要時間の差は ５－２＝３分で、これが⑤と⑥の差の①にあたるから、⑤にあたる時間は３分×５＝15分です。 →分速90ｍで行くときの所要時間

家から学校まで15分で着いて始業時刻の５分前だから、学校の始業時刻は８時＋15分＋５分＝８時20分
学校までの距離は解き方１と同様に90(m／分)×15分＝1350ｍと求めることができます。

みなさんはどちらの解法を支持したいですか？
僕は中学受験の算数を教え始めて二十数年たちますが、これをどちらで教えるかはいまだに悩ましいです。みなさんの頭になじむ方で解いてくれてよいですが、受験に向けていろいろな算数の問題に対応していくためには、解法のポケット(引き出し)は多い方がよいでしょう。自分の家の卵焼きが塩味で、あまり卵焼きを好きになれなかった子供が、友だちの家で甘い卵焼きを食べて卵焼きの美味しさに感激した……　僕の師匠がよく父母会で使っていた話ですが、算数をなかなか好きになれなかった生徒が、ある問題のある解き方をすごく気に入って、それをきっかけに算数が大好きになって成績がどんどん伸びたというケースはけっこうありますよ。算数に強くなるためにはいろいろな解き方を知ってほしいですね。

今回はあとがきが長くなりました。それではみなさん、また次の講座でお会いしましょう！もしよかったら、どちらの解き方が好きかコメントらんから教えてくださいね。

カーテンコール
始業時間まで歩いたと仮定して、行きすぎちゃうとか手前にいるとか差集め算を使う解き方もありますが、僕の経験ではあの線分図は生徒の理解があまりよくないです。