NEWみんなの算数講座92 高校の公式に算数が挑む！

みなさんこんにちは。ニューみん算講座92回目です。
今回の講座は少し難しいと思います。高校で習う公式を算数で説明してみよう！という企画テーマです。今日ここで高校の頃詰め込みで覚えた公式の意味がわかり、スッキリする人がいらっしゃるかもしれません。

ではさっそく始めますが、今回の内容が算数でダイレクトに使えることは少ないでしょう。しかし考え方のナルホドさはスゴいですよ？ぜひじっくりとお読みいただき、算数の知恵に感動していただきたいと思います。

今回の本題を説明する前に、ひとつ準備運動をしましょう。この準備運動は算数でもよく使います。

１、２、３、４、５、………、Ｎ
これをすべて加えるときは、逆の順番に並べた数列と組み合わせるのがうまい方法です。終わりがＮだとわかりにくいと思うので、１から10までの和を例にしてみます。

１＋２＋３＋４＋５＋６＋７＋８＋９＋10＝？

１、２、３、４、５、６、７、８、９、10　←知りたいのはこの和！
10、９、８、７、６、５、４、３、２、１　←下に逆の順の数列を書く

このようにして、上下の数列の各項を加えてみてください。すべて11になりますね？
11が何組できますか？　そう、10組ですよね。11を10倍して110。
しかしこれで終わりにしてしまうと、下の数列までたされてしまうから、最後に「÷２」をすると上の数列だけの和になります。上下の数列は順番は逆ですが、同じ内容の数列だから「÷２」で問題ないですね。１から10までの整数の和は110÷２＝55です。

このことから、１からＮまでの整数をたすときは、次の①～③の計算をすればよいことがわかります。下に公式を載せておきますね。
①１と最後の数をたす　～上の例では１＋10
②最後の数をかける　～上の例では「×10」
③２で割る

いま例で用いた「１から10までの和55」は、算数の勉強では一般常識のようによく使いますから暗記してくださいね。
＊１からＮまで加えた整数の和を三角数といいます。Ｎ＝１からＮ＝15までの三角数は次の通りです。
１,３,６,10,15,21,28,36,45,55,66,78,91,105,120

さてここからが今回の本題です。準備運動は１からNまでの整数の和でしたが、次のような和はどうなるでしょう？

中学受験生の人で知っている人はかなり少ないと思いますが、ご両親や高校大学のごきょうだいなら知っている人が多いかもしれません。これは高校の数学で勉強する２乗和という内容なのです。先に答えを発表しますね。公式はこうなります。

ためしにNに10をあてはめてみましょうか。
10×(10＋1)×(10×２＋１)÷６＝10×11×21÷6＝385

385と出ました。これが１（＝１×１）、４（＝２×２）、９（３×３）、16（４×４）、25（＝５×５）、36（＝６×６）、49（＝７×７）、64（＝８×８）、81（＝９×９）、100（＝10×10）をすべて加えた和です。電卓を使ってたしてみてください。納得しておいてもらえると話がしやすいです。

では冒頭で予告したように、この２乗和の公式を算数で説明しますよ？

Ｎはいくつにしても同じですが、ここではＮ＝４、つまり
１×１＋２×２＋３×３＋４×４の例で話をします。

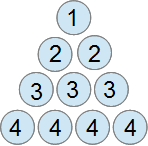
このように、ボーリングのピンのように数字を書いてみます。Nを４にしたのはボーリングという言葉を説明で使いたかったのもあります。
さて、このボーリング図。１が１個、２が２個、３が３個、４が４個ですね？
ということはこの数字の合計が１×１＋２×２＋３×３＋４×４の答えです。

この式を普通に計算するのでは、ここでは意味がありません。なぜなら、１×１＋２×２＋３×３＋４×４……＋100×100だったら普通には計算できませんよね？いつでも使える公式が欲しい！

そこで算数の知恵！　上のボーリング図のトップピン（１のピン）を左下にした図と右下にした図を用意します。愛用ソフトで作りました。上の図といっしょに並べますね。

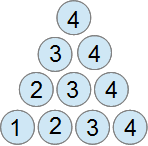
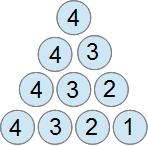
３つの図の一番上のピンをみてください。
左の図から順に　１　４　４　です。
その合計は９（＝１＋４＋４）ですが、それはどの位置にあるピンでも同じになりませんか？
たとえば一番下段の左から２番目のピン。
左の図から順に　４　２　３
合計するとやはり９です。
じつは３つの図で同じ位置あるピンは、どの位置でたしてもすべて９なのです。

この９の意味は、最初の数の１と、最後の数の４を２個たした合計。つまりワクで囲んだ公式の （Ｎ×２＋１） の部分です。
この９を10倍すれば（ピンは10本だから）、上の３つのボーリング図の数字の総合計になります。９×10＝90です。
しかしそのままでは３つの図の合計になってしまうので、90を3で割って、１つのボーリング図の数字の合計、つまり１×１＋２×２＋３×３＋４×４の答えは90÷３＝30です。

では今の考え方を、いつでも使える公式として残しましょう。
①３つのトップピン（一番上のピン）の合計は１＋N＋N。この式を整理してＮ×２＋１です。
②１つの図のピンの本数は、準備運動で説明した１からNまでの整数の和、すなわち（Ｎ＋１）×Ｎ÷２です。
③①と②をかけると、３つの図の総合計になるから、「÷３」をして１つの図の合計にします。

以上①、②、③をまとめると、
（Ｎ×２＋１）×（Ｎ＋１）×Ｎ÷２÷３
各項を長さの順にバランスよく並べ、÷２÷３を÷６にまとめると、さきほどの公式が出てきます。
１×１＋２×２＋３×３＋４×４＋５×５＋……＋Ｎ×Ｎ
＝Ｎ×(N＋１)×(Ｎ×２＋１)÷６

以上高校の数学で習う２乗和の公式を算数の範囲で説明することに成功しました！

＊＊＊
どうでしたか？　むかし本で読んだ内容なので、僕のオリジナルではないです。しかしこの算数の知恵には感動を覚えるものがありませんか？算数って素晴らしいですね。
え？３乗和ですか？　３乗和でも４乗和でも公式はずっとありますよ。興味のある方は「ファウルハーバーの公式」で検索してみてください。ここにも少しだけ載せておきましょう。２乗和以上に算数では使いませんが、数の世界に興味を持っていただけたらうれしいです。

３乗和
N×N×（N＋１）×（N+1）÷４
＊指数表記をすると{N×（N＋１）}²÷４
＊不思議なことに、準備運動の「１からNまでの和の公式」自体が２乗されています。

４乗和
N×（N＋１）×（Ｎ×２＋１）×（N×N×３＋N×３－１）÷30
＊前の方は２乗和と似ています。

では今回の講座はここまでにしたいと思います。前回から始めた次回予告をしましょう。次回は「仕事算」を書きます。どうぞお楽しみに！

インフォメーションボード

〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。

〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。

〈算数講座へのご意見や質問／ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。

〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、５講座ずつを１冊子にまとめ、「なかとじ印刷」した片側Ａ５サイズ（開くとＡ４）のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら