Newみんなの算数講座36 方程式の弟マルイチ算

みなさんこんにちは。前回に続いて今回も初めて発表する新作講座です。元祖の講座23、35、36は充実したリニューアルを目指して自らボツにしました。元祖の講座数は100を超えていますが、この先にもボツによる新作差し替えが出るかもしれません。まだ先が長いのでいつ出るかは未定ですが(笑)

では新作講座36です。これはいつか書かなくてはならないと前々から思ってました。方程式を使わないと言われる算数ですが、完全に100％排除しているわけではないんです。算数のお兄さんが数学だとすれば、お兄さんの長所を弟としてまったく無視できないという感じでしょうか。今回は数学の弟算数が方程式をアレンジしたマルイチ算についてお話しすることにしましょう。

塾のテキストや参考書で、①、③、⑥のように線分図の数字が〇で囲まれているのを見たことがあると思います。〇の中は整数だけには限りませんね。小数や分数が囲まれていることもあるでしょう。あの数字は割合や比を表す数字なのですが、あのように数字を〇で囲む書き方が方程式で使うＸと無関係ではないのです。わかりにくいかな？ まぁ先を読んでください。

線分図である量が③と示されているとき、その③が整数の３ではないことはおわかりだと思います。問題によって③と整数の３がたまたま一致することはあるかもしれませんが、③の示す量が48kmであったり、225cm²であったり、1200円であったりするのは普通です。３で割りきれる例を並べましたが、場合によっては③＝500リットルのように割りきれないこともあります。算数でよく見かける③というのは整数の３ではなく、基準量(①にあたる量)に３をかけた量なのです。基準量がきれいな整数の方が解く人は気分がよいですが、あいにく小数だったり分数だったりすることも少なくありません。

話を進めます。
３を基準量にかけること。数学だったらどう表現するでしょうか。基準量がわかっていないときは３×Ｘと表現しますよね？ ここでひとつ大事なことをお伝えできますよ。じつは算数でよく見かける③とはまさに数学の３×Ｘ (３Ｘ) のことなのです。

では簡単な問題を１問。問題は簡単ですが、数学とはちがう算数の書き方を知ってくださいね。

方程式とマルイチ算の両方で解いてみますね。

方程式
長女の年令をＸ才として、３Ｘ＋４＝43という方程式を立てるでしょうね。
３Ｘ＋４＝43　(＋４を移項して)
３Ｘ＝43－４
３Ｘ＝39　(両辺を３で割って)
Ｘ＝13　答え 13才
無事に解けています。これはこれで問題ないですね。

マルイチ算
長女の年令を①とします。算数でよく使う①というのは方程式のＸと同じ役目なのです。方程式でＸとおくところを算数では①にする。そう覚えてもらって大丈夫です。また、Ｘを３倍すれば３Ｘになるように、①は３倍すれば③になります。式はこうなります。
③＋４才＝43才
この式を逆算すれば
③＝43－４＝39才　(３で割って)
①＝13才　答え 13才
算数にはイコールをまたぐと＋－の符号が変わる移項という概念はないですが、普通に逆算すれば簡単ですね。方程式には単位を省く習慣がありますが、算数では必要に応じて式にも単位をつけてください。具体的な量であることがより明確になりますからね。

では少しレベルを上げて２問目。今度はマルイチ算独特の式の処理にも注目してください。

方程式
子どもの人数をＸ人としてピノの総数を２通りに表してイコールでつなぐのが普通でしょう。
３Ｘ＋45＝５Ｘ－７　(Ｘの項は左辺に、定数項は右辺に集めます)
３Ｘ－５Ｘ＝－７－45
－２Ｘ＝－52　(両辺を－２で割って)
Ｘ＝26　答え 26人

マルイチ算
子どもの人数を①としてピノの総数を２通りに表してイコールでつなぎます。
①×３＋45人＝①×５－７人　(①の３倍は③、５倍は⑤です)
③＋45人＝⑤ー７人
算数には移項やマイナスの数はないから、イコールの両側の「比の数の差」と「実際の量の差」が等しいと考えます。「比の数の差」は②、「実際の量の差」は加えた45人と引いた７人の差だから52人です。比の数が右辺で②多いぶん、実際の量が左辺で52人多いわけですね。
②＝52人　(２で割って)
①＝26人　答え 26人

途中をもっとていねいに説明すると次のようになります。
③＋45人＝⑤ー７人　(両辺に７人をたすと右辺の－７人が消えます)
③＋45人＋７人＝⑤－７人＋７人
③＋52人＝⑤　(両辺から③を引くと左辺の③が消えます)
③－③＋52人＝⑤－③
52人＝②　(２で割って)
①＝26人
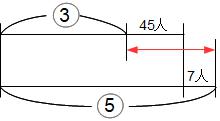
ここまでやらなくてもだいたいの生徒は上のピンク下線の説明でわかりますね。式だけの処理で不安なら下の線分図もご参考ください。赤い線に注目すれば②＝52人ですね。

もう１問いきましょう！かっこのはずし方は方程式もマルイチ算も共通です。

方程式
弟がもらったおこづかいをＸ円にしましょうか。
２(2500＋Ｘ)＝10000－1/2Ｘ　(かっこをはずす)
5000＋２Ｘ＝10000－1/2Ｘ　(分数を消すために両辺を２倍)
10000＋４Ｘ＝20000－Ｘ　(－Ｘを左辺に、10000を右辺に移項)
４Ｘ＋Ｘ＝20000－10000
５Ｘ＝10000
Ｘ＝2000　答え 2000円

マルイチ算
兄が使った金額を①円、弟がもらった金額を②円としましょう。
(2500円＋②)×２＝10000円－①
算数でも分配法則を使ってこのかっこをはずす勉強はします。
2500円×２＋②×２＝10000円－①
5000円＋④＝10000円－①
さきほどと同じようにイコールの両側の「比の数の差」と「実際の量の差」が等しいと考えます。「比の数の差」は加えた④と引いた①の差だから⑤です。「実際の量の差」は5000円です。
⑤＝5000円　(５で割って)
①＝1000円
弟がもらったおこづかいは②だから
②＝1000×２＝2000円　答え 2000円
＊弟がもらった金額を①にすると、兄が使った金額は1/2を〇で囲めばよいです。分数を避けるために兄が使った金額を①にしてみました。比はこのあたりも柔軟性がありますね。

こんなふうに、方程式でＸとおくところを①として問題を解くことは算数でもあるんです。Ｘを求めるのではなく①を求めるからマルイチ算と呼ばれてますね。方程式のアレンジですが方程式とまでは言えないでしょう？ マルイチ算という名前、ぜひ覚えておいてください。算数には０より小さいマイナスの数と移項がないから、式を作ったあとの処理に多少の慣れが必要ですが、慣れてしまえば特に難しい処理ではないと思います。イコールの両側の「比の差」と「実際量の差」が等しくなるのがポイントですね。イコールの両側で＋と－に分かれているときは「たした数」が差になります。

では今回の講座はこのへんで………の前に、これはどうしても付け加えておきたいのですが、算数の文章題にはマルイチ算を使わなくても解ける方法が必ず用意されています。たとえば今回の２問目は講座13で解説した過不足算ですし、３問目もマルイチ算で押し通すより線分図といっしょに考える方が算数らしいです。何度か書いたことですが、算数の目的は柔らかい思考力の養成だから、式だけで済ませようとこだわってほしくないのです。もちろんマルイチ算がダメとは言いませんし、使えるときは使ってくれてもよいですが、それですべてが解決するほど算数の文章題はたやすくないですからね。他の解き方を知ろうとする姿勢をいつも忘れないでくださいね。

では今回の講座はこのへんで！今度はほんとに終わります(^^♪

カーテンコール
方程式でＸ以外に文字を使うならＹですね。ＸとＹの連立方程式を勉強した人は多いでしょう。算数で〇囲み以外の割合や比を表現したいときは□で囲んだ数を使います。もし３つめのＺが必要なら△で囲みますね。その順番にきまったルールはないですが、〇→□→△の順番は守っている先生が多いようです。ただし、こうしたマークが混在するほど事後処理は複雑になります。２つめの□はたまに見ますが、３つめの使用は算数では相当レアですね。今回はシンプルに〇だけで収まる問題を取り上げました。