Newみんなの算数講座38 マジョリティーとマイノリティー

今日も僕の算数を読みにきてくれてありがとうございます。講座38を始めます。
今回は講座14以来、算数に２つの英単語が登場しますよ。算数の勉強にもなり、いつか役に立つ英単語まで覚えられちゃう。一石二鳥の算数講座ですね(笑)

それでは最初に今回の主役になる２つの英単語を紹介します。若い人はあまり使わないだろうけど、大人の世界ではときどき使われる単語です。

ｍａｊｏｒｉｔｙ
ｍｉｎｏｒｉｔｙ

読めますか？ そっかそっか、タイトルにカタカナで書いたから読めますよね。上がマジョリティーで下がマイノリティーです。意味はマジョリティーが多い意見、マイノリティーが少ない意見です。たとえばこんなふうに使います。「大阪は府のままでいいというのがマジョリティーだろうけど、自分は大阪都が実現してほしいと思ってるんだ。マイノリティーだね」この講座を最初に書いた頃から大阪を東京に続く第二の都(ト)にしようという話がありました。実現には至りませんでしたね。

さて話を算数に戻して、これがいったい算数とどんな関係があるのか？ ではその話をしましょう。

みなさんは、最大公約数や最小公倍数をどのように計算しますか？ 割り算みたいな筆算で計算する連除法(れんじょほう)でしょうか。実際、学校や塾ではほとんど連除法だけかも知れません。では例題を出しますからやってみてください。

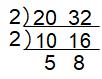こんなふうに書いて計算しましたか？ これが連除法ですね。左にある割った数だけをかけると最大公約数、下の数まで全部かけると最小公倍数ですね。
答えは最大公約数が２×２＝４ 最小公倍数が２×２×５×８＝160です。連除法も使う人が多い立派なやり方だから、これはこれで覚えておいてくださいね。

でも今回の講座では別の方法を説明します。とても面白いやり方です。しっかり読んで覚えてくださいね。

まず、それぞれの数を素因数分解します。素因数分解とは素数の積の形で表すことです。＊講座１ 講座２参照
60＝２×２×３×５
96＝２×２×２×２×２×３

２、３、５という３種類の素数が出てきましたね。ではその種類と個数に注目して見やすく色別に直してみます。
60＝２×２×３×５
96＝２×２×２×２×２×３

さてここで今回のタイトルを思い出してもらって、最大公約数はマイノリティー、最小公倍数はマジョリティーと覚えてください。
つまり、60と96の持つ２、３、５の素数について、最大公約数を求めるときは少ない個数の意見を取り入れ、最小公倍数を求めるときは多い個数の意見を取り入れます。

ではマイノリティーの最大公約数からやってみます。
〔２について〕60に２個、96に５個あるから、少ない個数の意見で２個を採用します
〔３について〕60に１個、96に１個あるから、少ない個数の意見で１個を採用します(個数が等しいときは等しい個数でよい)
〔５について〕60に１個、96に０個あるから、少ない個数の意見で０個を採用します
このように採用した２を２個、３を１個、５は使わずにかけ算して、60と96の最大公約数は２×２×３＝12と求めることができます。

次にマジョリティーの最小公倍数をやってみます。
〔２について〕60に２個、96に５個あるから、多い個数の意見で５個を採用します
〔３について〕60に１個、96に１個あるから、多い個数の意見で１個を採用します(個数が等しいときは等しい個数でよい)
〔５について〕60に１個、96に０個あるから、多い個数の意見で１個を採用します
このように採用した２を５個、３を１個、５を１個かけ算して、60と96の最小公倍数は２×２×２×２×２×３×５＝480と求めることができます。

まとめますね。

最大公約数と最小公倍数を求めるマジョリティーとマイノリティーの考え方、いかがでしたでしょうか。けっこう楽しいでしょう？ こうした話は塾などでもあまり聞けないと思うし、のってる参考書も多くないと思います。この講座ではこれからもこうした秘技をいろいろ紹介していこうと思います。気分次第でどこの講座にどんな秘技を書くかわからないので、なるべくたくさんの講座を読んでくださいね。え？難しいって？ そっか～。ちょっと説明を急いだかもしれませんね。でも大事なことは書き忘れてないから、もう一度じっくり読めばきっとわかると思います。パソコンやスマホで読むのではなくて、カラー印刷して読むのが一番いいかもね。
では今回の講座38はこれでおしまいです。なるべく早いうちにまた次の講座で一緒に算数を楽しみましょう。

カーテンコール
連除法がまるで役に立たず、この方法を知らないと解けない整数問題があります。その問題をみなさんへの宿題に選んでみました。この講座をフル活用して考えてみてください。