Newみんなの算数講座56 何個壊れて何個無事?

みなさんこんにちは。ニューみん算講座56を始めます。
今回の講座は、立方体を積み上げるところまでは講座15と似ています。講座15は積み上げてから色を塗りましたが、今回は積み上げてから包丁で切断して、小さな立方体が壊れるのか無事なのかを考えます。とても面白い問題ですよ。
問題を出す前に少しだけ講座づくりの舞台裏…。図形の講座を書くときは図形作成ソフトを使うのですが、昔書いた講座を改訂していて、下手だったな~と思うことが多いですね。いまでもプロとかの人に比べたら全然下手でしょうけど、昔に比べたらだいぶうまくなってきた気がします(*^^) これからも素人なりになるべく見やすい図を出せるように頑張りますね。
では今回の問題です。見やすい図ができたかな?
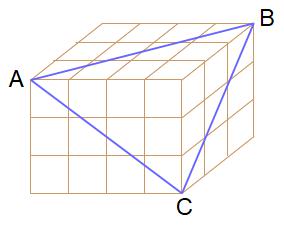
下の図のように64個(=4×4×4)の小立方体を積み上げて作った大きな立方体があります。この大きな立方体を3点ABCを通る平面で切断します。(切り口は正三角形)
このとき、64個の小立方体のうち、壊れる立方体と壊れない立方体はそれぞれ何個ですか?
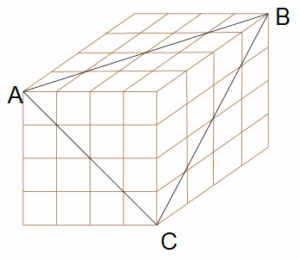
みなさんならこの問題、どのように考えますか? なんとなく見た目で判断しようととすると、けっこう頭がこんがらがります。壊れる、壊れないがハッキリと確認できるものもあるけど、ここはどっちだろう?と悩んでしまう微妙なものもあります。かなり空間センスに長けた人でも、見た目で答えを出すのは大変でしょう。
おススメはこんな考え方。
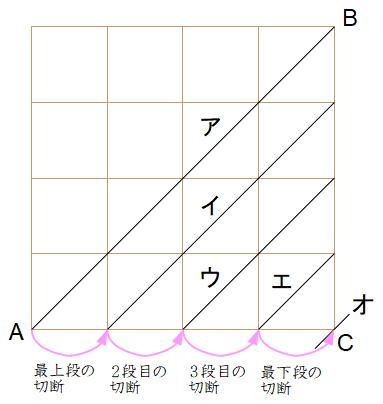
上の図のように、真上から見た平面図を書き、切断面の移動を斜め線で記入します。よほど複雑な問題でなければ1枚の図で足りると思います。
この問題の切断面は、一番上の段を斜め線アから切り始め、斜め線イまで進んだときに一番上の段を切り終えます。したがって、一番上の段で壊れる立方体は斜め線アとイの間にある7個です。
切断面は上から二段目を斜め線イから切り始め、斜め線ウまで進んだときに、上から二段目を切り終えます。上から二段目で壊れる立方体は斜め線イとウの間にある5個です。
このあとも同じです。切断面は上から三段目を斜め線ウから切り始め、斜め線エまで進んだときに、上から三段目を切り終えます。上から三段目で壊れる立方体は斜め線ウとエの間にある3個です。
一番下の段は、切断面が斜め線エから切り始め、最後は斜め線オまで進んで頂点Cから抜けていきます。一番下の段で壊れる立方体は斜め線エとオの間にある1個です。
以上のことから、壊れる小立方体は全部で7+5+3+1=16個。これを全体の個数から引き算して、壊れない小立方体は 64-16=48個です。
切断面を斜め線で追いかける考え方、楽しいでしょう? もっともいまの問題は、全体が4×4×4の立方体になっていて、どの段でも切断面が中途半端な場所を通らないから、空間センスがある人や勘のいい人なら見た目だけでわかっても不思議ないかもしれません。壊れる個数は7→5→3→1と規則的ですし…。でも全体の形が変わると見た目での判断は難しくなりますよ。たとえば次のような問題。
最初の問題と同じようにABCを通る平面で切断したとき、壊れる立方体と壊れない立方体の個数をそれぞれ求めてください。
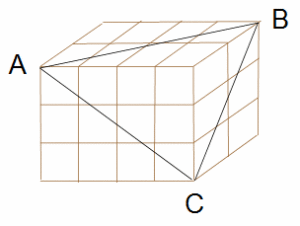
今度は最初の問題と違い、全体が立方体ではないため、切断面が小立方体の頂点ではない中途半端なところを通ります。全体の個数は2×4×3=24個で最初の問題より少ないですが、見た目での判断はこちらの方が難しいでしょう。
さきほどと同じように上から見た平面を書いて切断面を追いかけますが、各段ごとの通過点を慎重に考えてください。
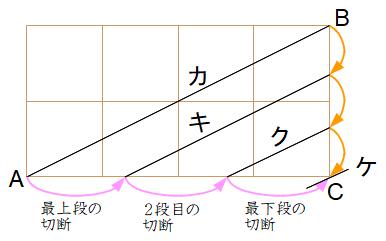
ピンクとオレンジの線はAC、BCをそれぞれ3等分しています。問題の直方体はタテ2、横4に対して高さが3だから、タテは1段に対して2÷3=2/3マス(小数だと約0.7マス弱)進み、横は1段に対して4÷3=4/3マス(小数だと約1.3マス強)進みます。
切断面は、一番上の段を斜め線カから切り始め、斜め線キまで進んだときに一番上の段を切り終えます。一番上の段で壊れる立方体は斜め線カとキの間にある6個です。
切断面は、上から二段目を斜め線キから切り始め、斜め線クまで進んだときに上から二段目を切り終えます。上から二段目で壊れる立方体は斜め線キとクの間にある4個です。
切断面は、一番下の段を斜め線クから切り始め、最後は斜め線ケまで進んで頂点Cから抜けていきます。一番下の段で壊れる立方体は斜め線クとケの間にある2個です。
これらのことから、壊れる小立方体は全部で 6+4+2=12個。これを全体の個数から引き算して、壊れない小立方体も 24-12=12個です。半分壊れて半分壊れないのですね。(数値設定による偶然です)
以上立体切断戦争における負傷者と無事だった人の数のレポートでした(笑)
どうでしたか? よくわかったって? それはきっとボクの説明がうま… じゃなくて、みなさんがだんだん算数に強くなってきた証拠でしょうね。だってもう56個目の講座ですもん。じつは小学生の算数でも中高生の数学でも、生徒の理解が一番悪いのは何を隠そう立体図形です。立体という高さを持ったものを無理やり平面に収めて考えてますからね。苦労するのも当たり前と言えますが、入学試験etcで出されるの問題は限られたパターンですからね。よく出る問題のレパートリーを少しずつ広げていくことで得点できるチャンスは増えていきますね。
ではこれで講座56は終わりです。次回は船が川を上り下りする流水算を解説したいと思います。ではまたそのときにお目にかかりましょう!
カーテンコール
壊れる立方体も壊れない立方体も、斜め線の移動順に別の段の様子を考えています。たとえば最初の問題でアとイの間の壊れる立方体と、イとウの間の壊れる立方体は別の段(一番上の段と二段目)に存在しています。段ごとに図を書き直してもよいですが、特に混同のおそれもないと判断し、1枚の平面図に収めて解説しました。
みなさんへの宿題
下の図のように、立方体を36個積み上げて作った直方体があります。(3×4×3=36個) この直方体を三角形ABCを切り口として切断したとき、壊れる立方体と壊れない立方体はそれぞれ何個ありますか?
解答したい方はページ下のコメントに書いてください。正解不正解をレスさせていただきます。お名前はニックネームでもかまいません。
-
前の記事

Newみんなの算数講座55 連続数による和分解
-
次の記事

Newみんなの算数講座57 流水算のルール











