Newみんなの算数講座58 帰ってきたてんびん

みなさん、こんにちは。ニューみん算講座58です。

この講座の初期に食塩水のてんびんについて書きましたよね？(講座３) あれは、食塩水と言えばてんびん、てんびんと言えば食塩水というぐらい有名な考え方ですけど、じつはてんびんが使える問題は食塩水だけではないんです。僕はウルトラマン全盛世代ですから、今回の講座を帰ってきたてんびんというタイトルにしましたよ(*^^) ではてんびんが活躍できるもうひとつのジャンル、平均算という文章題のお話を始めますね。

さて平均ってなんでしょう？
シンプルすぎて、言葉で説明しようとすると考えてしまいます。たとえばみなさん【左】ってどう説明します？ 左手の方向では左がふくまれていて説明にならないです。以前本を書いていて困ったことがあり、辞書を引いてみたのですが、なんて書いてあったと思います？ 左は「右の反対」だって(笑) 説明になってないと思ったけど、単純すぎる言葉の説明は辞書を書く人でも悩むのでしょうね。これとまったく同じ話が映画「舟を編む」に出てきたときは驚きました。世の中、同じことを考える人がいるんですね～(^^)/

すいません脱線してしまいました。平均も説明しにくい言葉ですが、平均の均という字は訓読みで「なら(す)」と読みます。平らに均す。均して平らにする。説明としては次のようにまとめておきますね。

言葉で説明すると手こずる平均ですが、イメージとしてはちょうど真ん中、可もなく不可もなく…というイメージですよね。では平均算の問題を出しますよ？ 難しくないですが、経験がないと解きにくい問題かもしれません。

とてもよく見かける平均算です。平均算には有力な解き方がいくつかありますが、この問題は面積図で解いてみましょう。平均にデータ数をかけると全体での合計になります。このことはいろいろな問題でとてもよく使われます。

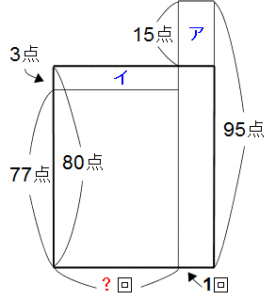
算数の重要キーマンの面積図！ タテの線が平均点、横の線がテストの回数を示しています。今までのテストの回数がわからないから？回です。
左側の長方形の面積は77点×？回。この面積が今までのテストの合計得点です。また、右側の長方形の面積が95点×1回で、これが次の95点のテスト(１回)です。
左右の長方形を平均化させて太線で囲んだ長方形にするとき、イの長方形がアの長方形に組み込まれて平均化します。つまりアの面積とイの面積は等しいです。
80－77＝３
95－80＝15
３×？＝15×１
この式から？＝５とわかり、今までのテストの回数は５回です。これに１を加えて次回のテストは６(回目)です。

では次の問題です。てんびんが久々に帰ってきますよ？

この問題も面積図で対応することはできますが、ここでは講座３以来久々にてんびんに帰ってきてもらいましょう。食塩水の問題でよく使うてんびんは、このような平均算にも使うことができます。
＊食塩水のてんびんを知らない人は講座３を読んでください。

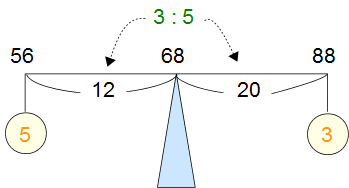
ウデの左端に２軍の平均点、右端に１軍の平均点を書き、中央に全体の平均点を書きます。
支点中央から両端までの長さの比は、
(68－56)：(88－68)＝12：20＝３：５ ←緑の数字

両端のおもりがそれぞれのクラスの人数にあたります。
てんびんの性質より、ウデの長さとおもりの重さは逆比の関係があるから、
二軍の人数(左のおもり)と一軍の人数(右のおもり)の比は５：３になります。←オレンジの数字

６年生全体の56人を５：３に比例配分して、二軍の人数は56×5/8＝35人、一軍の人数は 56×3/8＝21人です。

以上今回は　面積図とてんびんを１回ずつ使って平均算の解説をしました。みなさんは面積図派かな？てんびん派かな？
テストの回数と平均点、２つのグループの人数と平均点が絡んだ問題は、だいたい今回のような解き方で解決できるでしょう。解説と逆に、初めの問題をてんびん、２問目を面積図を使って解いてみると、よりいっそう平均算の理解が進むのではないかと思います。

では講座58はここまでです。次の講座は元祖を改訂するか、新しく差し替えるか考え中です。なるべく早いうちに決めて発表したいと思います。またみなさんに算数のお話ができる機会を楽しみにしています。ではまた～！