NEWみんなの算数講座91 歯車の話

こんにちは。前回で節目の90講座に到達し、ここからは100講座へ向けて前進です。今回は歯車の話をしようと思います。
 歯車を言葉で説明するとなると悩んでしまいます。ウィキペディアから説明を借りてきました。
歯車を言葉で説明するとなると悩んでしまいます。ウィキペディアから説明を借りてきました。
〈歯車とは動力の伝達に用いられる機械の要素。英語ではギヤ〉
となってました。さすがウィキペディアは説明がシンプルで上手ですね。
もう少し意味をつけたすと、歯車の役割は、歯の数が違う歯車をかみ合わせることで、小さな力を大きな力に変更したり、スピードを速くしたり遅くしたりするということでしょう。身のまわりではクルマの部品に歯車が使われてそうです。最近は見なくなりましたが、ぜんまい式の時計を分解すると内側は歯車だらけでした。携帯電話の中にも歯車は使われているようですよ。歯車も小型化が進んでいて、今は1マイクログラム(=100万分の1グラム)の歯車もあるのだそうです。
さていったい歯車がどのように算数の問題とつながるのでしょうか?
ではこれから3問の問題を通して、算数でよく出される歯車問題を知ってもらうことにしましょう。
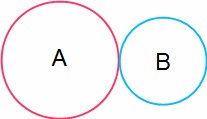 右の図のように、かみ合って回っている歯車A、Bがあります。Aの歯の数は56、Bの歯の数は40です。Aが20回転するうちに、Bは何回転するでしょうか?
右の図のように、かみ合って回っている歯車A、Bがあります。Aの歯の数は56、Bの歯の数は40です。Aが20回転するうちに、Bは何回転するでしょうか?
基本問題から入りました。まず押さえてほしいことは、かみ合って回っている2つの歯車は、歯の数(イラストにはありませんが歯車のギザギザの数のことです)と回転数(同じ時間での)が逆比の関係になります。比を習っていない学年の人は、倍率が逆になると考えてくれても大丈夫です。
比で考えてみると、AとBの歯の数の比は56:40。8で割って7:5です。
*比の両側は0以外の同じ数で割ってよい
すると回転数は逆比の5:7になるから、Aが20回転する時間で、Bは20÷5×7=28回転することになります。
倍率で考えるなら、Aの歯の数はBの歯の数の56÷40=56/40=7/5(5分の7)倍です。すると回転数は倍率が反対になり、BがAの7/5倍です。
Aの回転数が20回だから、Bの回転数は20×7/5=28回です。
大きい歯車は、歯の数は多いが動きが遅くてあまり回らず、小さい歯車は、歯の数は少ないが動きが速くてよく回る。イメージとしてはそういう理解でよいと思います。
では2問目。
下の図のように、歯車AとB、歯車BとCがかみ合って回っています。Aの歯の数は60、Bの歯の数は40、Cの歯の数は90です。Aが30回転するうちに、BとCはそれぞれ何回転するでしょうか?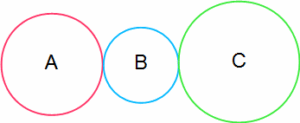
さっきと同じように歯の数の比を考えてみます。
A、B、Cの歯の数の比は、60:40:90=6:4:9です。この比の逆比が回転数の比になるわけですが、3つ以上の項がある連比(れんぴ)を逆比にするときは、2つの比のように数字をチェンジするのではなく、全部を逆数にして作ります。
*逆数…1をその数で割った商のこと。分母と分子を入れかえた数。(算数界の専門用語コーナーにも書いたことがあります)
A、B、Cの回転数の比は、6:4:9を全部逆数にして
1/6:1/4:1/9
分母を最小公倍数の36で通分して
6/36:9/36:4/36
36をかけて分母を消すと6:9:4。これが6:4:9の逆比、すなわちA、B、Cの回転数の比です。
あとはAの回転数が30回とわかっていますから、Bの回転数は30÷6×9=45回、Cの回転数は30÷6×4=20回と求めることができます。
AとCは直接かみ合ってはいませんが、Bを介(かい)して間接的にかみ合っていることになり、もしBの歯車を無視して、AとCの2つの歯車だけで歯の数と回転数を調べても、やはり逆比の関係になります。
AとCの歯の数の比 60:90=2:3
AとCの回転数の比 30:20=3:2 間違いないですね。
では最後に少しややこしい3問目。
下の図のように、4つの歯車A、B、C、Dからなる装置があります。それぞれの歯の数はA、B、C、Dの順に72、48、90、64です。Aが100回転するうちに、B、C、Dはそれぞれ何回転するでしょうか?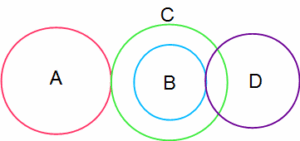
この問題では「かみ合っている歯車」と「乗っかっているだけの歯車」の区別が大事です。
上の2問で解説したように、かみ合っている歯車どうしは歯の数と回転数が逆比になりますが、BとCのように乗っかっているだけの歯車どうしではその関係はありません。
まずAとCはかみ合っていますから、AとCの歯の数の比72:90(=4:5)を逆比にして、回転数の比は5:4です。
Aが100回転すると、Cは100÷5×4=80回転します。
ここでBとCについて考えます。BとCはかみ合っているのではなく、BがCに乗っかっているだけだから、BとCは同じ時間内に同じ回数だけ回転します。つまりCが80回転すれば、Bも80回転します。
*乗っかっている歯車は回転数が等しい
次にBとD。
BとDはかみ合ってますから、歯の数の逆比が回転数の比です。BとDの歯の数の比は48:64=3:4だから、BとDの回転数の比は逆比で4:3です。
Bが80回転するとき、Dは80÷4×3=60回転します。
解答を整理します。
Aが100回転するとき、BとCはともに80回転、Dは60回転です。
***
今回は歯車の問題について解説してみました。ポイントは次の3点です。
●かみ合っている歯車どうしは、歯の数と回転数が逆比になる
●直接かみ合ってなくても、他の歯車を介して間接的にかみ合っている場合も、歯の数と回転数は逆比になる
●乗っかっている歯車は上下で回転数が等しい
そんなにしょっちゅう出る問題ではないと思いますが、どこかで出されたときに困らないようにしっかり覚えておいてくださいね。
なお、この歯車問題は反比例(小6算数・中1数学)という単元の題材としてもよく使われます。この講座では反比例という言葉は使いませんでしたが、逆比と反比例は密接な関係がありますので、説明の切り口が違っていても、この講座と似た内容を反比例の単元でも習うと思います。そのときもこの講座を思い出してくださいね。
では今回の第91講座はこのヘンでお開きにしようと思います。
次回の講座では、
1×1 2×2 3×3 4×4 5×5 ……を□×□まで加える計算方法をを算数の範囲で解説する予定です。珍しく次回予告などしてしまいました。どうぞ楽しみに!
インフォメーションボード
〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。
〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。
〈算数講座へのご意見や質問/ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。
〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、5講座ずつを1冊子にまとめ、「なかとじ印刷」した片側A5サイズ(開くとA4)のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら













