NEWみんなの算数講座80 ユークリッドの互除法

ニューみん算講座、今回で第80講座に到達です。まだまだ通過点のつもりですが、キリのよい数は気分がいいです。節目の今回は、長方形から正方形を切り取っていくユークリッドの互除法（ごじょほう）についてお話をしましょう。僕も最初に知ったときは スゴいことを思いつく人がいるな～ と感動した記憶がありますよ。

このテーマは長方形からスタートします。
まずは簡単な例で、タテ10ｃｍ、横15ｃｍの長方形にしましょう。その長方形の中に短い辺を１辺とする正方形を書きます。はじに寄せて書きますよ。図があったほうがいいですね。こんな感じです。

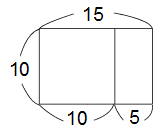
すると当たり前ですが、タテ10ｃｍ、横５ｃｍの長方形が残ります。その長方形の中に、初めと同じように短い辺を１辺とする正方形を書きます。

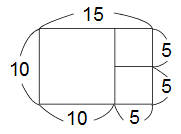
こうなりますよね？
初めの長方形がきれいにすき間なく正方形に分割されました。

そのときここで重大な事実！このように正方形だけに分割できたとき、

10と15の最大公約数は５。間違いないですね？

もう１つ試してみましょうか。
今度は初めの長方形をタテ84ｃｍ、横120ｃｍにしますね。

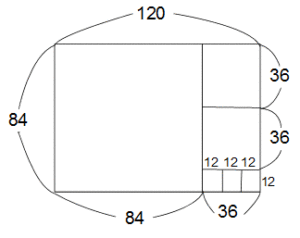
まず１辺84ｃｍの正方形を１個収め、残った長方形の中に１辺36ｃｍの正方形を２個収めます。そして最後に１辺12ｃｍの正方形を３個収めると、初めの長方形が正方形だけに分割できますよ。
最後に収めた正方形の１辺12ｃｍが、初めの長方形のタテ（84）と横の長さ（120）の最大公約数です。また間違いなかったですね。

で、これがどうしたかといいますと、いま説明した２例は比較的簡単な数だから、普通に計算しても最大公約数はわかると思いますが、もしこんな問題があったらどうしましょう？

両方を割れる数にはなかなか気づかないでしょうから困っちゃいますね。

じつはこんなとき、いまの考え方がすごく役に立つのです。タテ689ｃｍ、横1007ｃｍの長方形で、いまと同じことをやると…
＊数値が汚いから図は作りませんので、手もとの紙に書きながら確認してみてくださいね。

ア）1007÷689＝１個あまり318ｃｍ
まず１辺の長さが689ｃｍの正方形が１個収まります。

イ）689÷318＝２個あまり53ｃｍ
次は〈689ｃｍ×318ｃｍ〉の長方形の中に、1辺の長さが318ｃｍの正方形が２個収まります。

ウ）318÷53＝６個　➡　あまりナシ
次は〈318ｃｍ×53ｃｍ〉の長方形の中に、1辺の長さが318ｃｍの正方形が６個収まります。

ここで初めの長方形が正方形だけに分割されるから、初めの長方形のタテ（689）、横の長さ（1007）の最大公約数は、最後に収めた正方形の１辺、つまり53とわかります。

ややこしいかな？　使いやすい知識としてまとめましょう。

一生懸命説明しましたが理解していただけたでしょうか？
今回説明した最大公約数の求め方はユークリッドの互除法と呼ばれています。教え子が志望校の説明会に行ったとき、算数担当の先生がこの問題をプリントして配ったのだそうです。それを見せてもらいまして、これは講座に書かなくては！と思いました。これからも入試の題材になって不思議ないでしょう。みなさん、ユークリッドの互除法をぜひ覚えておいてくださいね。

では節目の80回目の講座はこれで終わりにします。ここまでくると100回目も見えてきました。一歩一歩前進します。また次の講座で一緒に算数しましょう！　それではまた！

NEWみんなの算数講座への質問やご意見、筆者ウタマル先生へのお便りは、メールのイラストをクリックして、メールフォームからお寄せください。