Newみんなの算数講座59 ニイチ君とサシゴ君

みなさんこんにちは~。今回の講座59は、旧ホームページ講座の改訂版ではなく、こちらのニュー講座用に新しく書いた新作です。新作はこの講座が6つめですね。右側サイドコラムにニュー講座新作というタグがありますから、よかったら使ってみてください。
今回の新作講座59では、平面図形の問題でとてもよく使われる2種類の直角三角形の区別をしようと思います。この2種類を混同している生徒をたくさん見てきました。同じ直角三角形だから似てる感じはありますけど、性質や使いどころは違いますからね。みなさんにはしっかり区別してほしいからこの講座を書いておくことにしました。
ではその2種類を順番に説明しましょう。僕の授業で呼んでいる名前で紹介しますね。一つめの直角三角形はニイチ君。二つめの直角三角形はサシゴ君です。
直角三角形ニイチ君
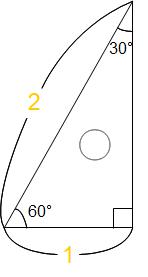
この直角三角形がニイチ君です。小学生のみなさんなら必ず持っている三角定規の片方ですね。直角以外の角は大きい方が60°、小さい方が30°です。
この直角三角形は60°をはさむ辺の長さが2:1になっています。2:1という辺の比が特長的だから僕の授業ではニイチ君と呼んでます。2:1になる理由は下の図のように2枚を左右対称に組み合わせると正三角形ができることから理解できると思います。
残る一辺(30°と直角の間)は、算数では使わないルート3(約1.73ぐらい)という数になるため、算数の問題で必要になることはありません。
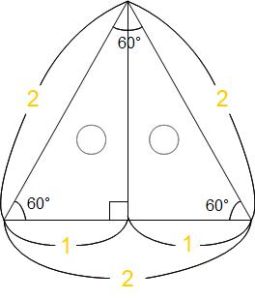
平面図形の問題で、直角三角形ニイチ君の2:1を使う問題はとても多いですよ。あとで出しますね。
続いて二つめの直角三角形サシゴ君について。
直角三角形サシゴ君
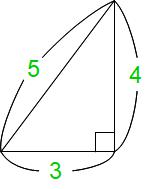
こちらがサシゴ君です。3辺の長さが3:4:5という連続するきれいな整数比になる直角三角形です。直角をはさむ短い方が3、長い方が4、直角と向かい合う辺(斜辺)が5です。3辺のうち2辺の長さ(cm)にこの比があてはまれば、残りの辺の長さを知ることができます。たとえば3の位置が6cm、5の位置が10cmなら残る辺は4に確定して8cmです。
この直角三角形サシゴ君に60°、30°を持ち出そうとする生徒がいますが、それはニイチ君との勘違いです。サシゴ君の直角以外の角は、算数では使えない無理数という数になってしまい、普通の整数、小数、分数で表現することはできないです。
*5と3がはさむ角は53°より少し大きい角度、5と4がはさむ角は37°に少し足りない角度です。高校数学の三角比で勉強する内容です。
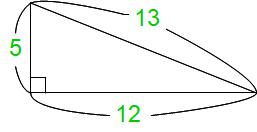
サシゴ君のように、直角三角形の3辺がすべて整数比になる場合は限られていて、算数でサシゴ君以外に出てくるのは5:12:13ですね。もう一つ8:15:17ものせておきますがあまり目にすることはないでしょう。3:4:5と5:12:13はかなり使えますから、ぜひ知識として覚えておいてください。
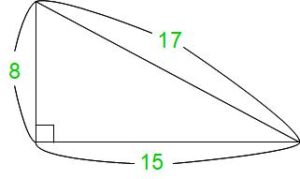
ではニイチ君とサシゴ君を使う問題を一問ずつ出してみますよ。
下の図は等しい辺の長さが8cm、頂角が30°の二等辺三角形です。この二等辺三角形の面積を求めてください。
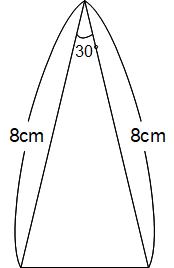
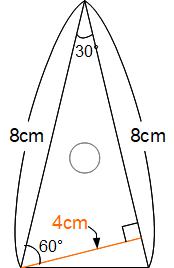
左下の頂点から右側の辺に垂直な線を引きます。すると二等辺三角形の内部にニイチ君が現れます。ニイチ君は60°をはさむ辺の比が2:1だから、垂直に引いた線の長さが4cmとわかります。この4cmは、二等辺三角形の底辺を右側の8cmをと見たときの高さになっているから、求める面積は8×4÷2=16cm²です。
下の図のような直角三角形ABCの頂点Aから辺BCに対して垂直な線AHを引きます。AH、BH、HCの長さをそれぞれ求めてください。
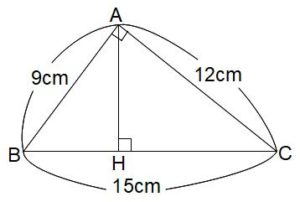
次のように同じマークをつけた角度が等しく、図の中の3つの三角形CBA(全体)、ABH(左側)、CAH(右側)はどれも相似な三角形です。 → 相似については講座23をご覧ください
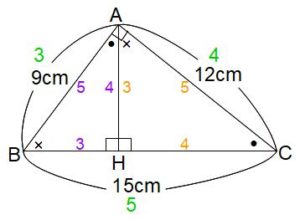
三角形CBAは3辺の長さがわかっていて、短い順に9cm、12cm、15cmです。この比が3:4:5になっているから、残り2つの三角形の3辺の長さも短い順に3:4:5です。
AHは三角形ABHの4にあたる辺で、5にあたる辺が9cmだから、AH=9cm×4/5=7.2cmです。
同様にBHは三角形ABHの3にあたる辺だから、BH=9cm×3/5=5.4cmです。
HCは三角形CAHの4にあたる辺で、5にあたる辺が12cmだから、HC=12cm×4/5=9.6cmです。 BHがわかればHCは引き算で求められますが、ここではあえてサシゴ君の比を使いました。
以上2種類の直角三角形ニイチ君とサシゴ君の紹介~例題でした。
直角三角形には中高の数学で勉強する三平方の定理(ピタゴラスの定理)が深く関係していて、その勉強のためにはルート(平方根)や二次方程式の知識が必要だから、そのどちらも扱わない算数では求められるものに限界があります。ニイチ君や正三角形の面積を求めることはできないし、サシゴ君の面積は大丈夫ですが角度(直角以外)を正確に知ることはできないです。
でも算数の図形の問題は、算数の範囲で解答できるギリギリまで踏み込んでくることがありますからね。今回の内容には中高の数学を使わないと説明しきれないことも含まれていますが、一般常識として知っておいてもらうことで、算数の図形の問題を解くときの余裕や助けになるだろうと思います。カーテンコールコーナーもぜひご参考くださいね。
それでは今回の講座59はこれで終わりにします。次回は旧ホームページの改訂作に戻りまして、速さのジャンルから美しき平行四辺形のグラフです。その講座でまたお会いしましょうね。みなさんお元気で~!
カーテンコール
算数のテストでの必要性は薄いですが、サシゴ君のように、すべて整数になる直角三角形の3辺の比を作る式を紹介しましょう。計算を楽しみながら数に親しんでください。
すべて整数になる直角三角形の3辺の比を作る式
【A²+B²】【A²-B²】【2×A×B】 (注)A²はA×Aです
この3つの式のA、Bにお好きな自然数をあてはめて計算してください。引き算があるからA>Bですね。どんな自然数を選んで計算しても、出てきた3つの数が直角三角形の3辺の比になります。本文にのせた比が出てくる例を書いておきますね。
〈例1〉A=2、B=1の場合
A²+B²=2²+1²=4+1=5
A²-B²=2²-1²=4-1=3
2×A×B=2×2×1=4
整数になる3辺の比 3:4:5
〈例2〉A=3、B=2の場合
A²+B²=3²+2²=9+4=13
A²-B²=3²-2²=9-4=5
2×A×B=2×3×2=12
整数になる3辺の比 5:12:13
〈例3〉A=5、B=3の場合
A²+B²=5²+3²=25+9=34
A²-B²=5²-3²=25-9=16
2×A×B=2×5×3=30
整数になる3辺の比 16:30:34=8:15:17
A、Bにあてはめる数を変えれば他にもたくさん作れますよ?(*^^)













