NEWみんなの算数講座82 そのとき花子

 今回のテーマは3人が池のまわりを回る旅人算なんですけど、そんなことできる池ってどこにあるんだろう?とジョークで書こうと思ったら僕自身がすごく気になってしまって…(笑)
今回のテーマは3人が池のまわりを回る旅人算なんですけど、そんなことできる池ってどこにあるんだろう?とジョークで書こうと思ったら僕自身がすごく気になってしまって…(笑)
ネットで探してみました。イメージとドンピシャなのは探せませんでしたけど、これなんかが近いですかね。熱海から30分の初島というリゾートアイランドにある池だそうです。写真をお借りした会社のページを貼っておきますね。
秋のエクシブ初島1泊
いつもと違う趣向で書き始めてみましたが、ここから算数の本題に入りますね。「そのとき花子」のはじまりです。タイトルの意味は読んでいるうちにわかると思います。
一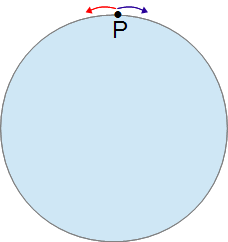 郎クン、二郎クン、花子さんの3人が、ある池のまわりの同じ地点(P)を同時に出発して池のまわりを回ります。一郎クンは左方向(図の赤い矢印)、二郎クンと花子さんは右方向(図の青い矢印)に回ります。
郎クン、二郎クン、花子さんの3人が、ある池のまわりの同じ地点(P)を同時に出発して池のまわりを回ります。一郎クンは左方向(図の赤い矢印)、二郎クンと花子さんは右方向(図の青い矢印)に回ります。
しばらくして一郎クンと二郎クンが出会い、その4分後に一郎クンと花子さんが出会いました。一郎クンの速さは毎分100m、二郎クンの速さは毎分80m、花子さんの速さは毎分60mです。この池のまわりの長さは何mですか?
パソコンを新調したら、前よりも図がきれいに作れた気がします。まぁ自画自賛は置いといて、さっそく解説を始めますね。
まず、一郎クンと二郎クンが出会ったときを考えてみます。そのときね、スポットライトを一郎クンと二郎クンだけにあてないで、花子さんがいる位置もチェックしておくことがとても大事です。
図と解説をいっしょにご覧ください。
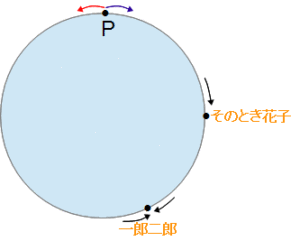 一郎二郎と書いてあるところが一郎クンと二郎クンが出会った地点。そのとき花子と書いてあるところが、一郎クンと二郎クンが出会ったときの花子さんの位置です。この花子さんの位置がとても重要です。これを書かないためにこの問題が解けない生徒が多いです。「そのとき花子」のチェックを忘れないでください。
一郎二郎と書いてあるところが一郎クンと二郎クンが出会った地点。そのとき花子と書いてあるところが、一郎クンと二郎クンが出会ったときの花子さんの位置です。この花子さんの位置がとても重要です。これを書かないためにこの問題が解けない生徒が多いです。「そのとき花子」のチェックを忘れないでください。
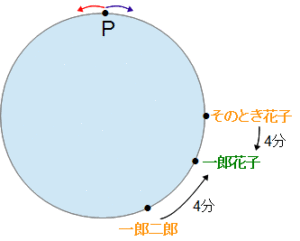 一郎花子と書いたところが一郎クンと花子さんの出会った位置です。一郎二郎から一郎花子までは、一郎クンが4分で進むきょりだから100×4=400m。また、そのとき花子から一郎花子までは花子さんが4分で進むきょりだから、60×4=240mです。これらを合計すると400+240=640m。これは一郎二郎からそのとき花子までのきょりです。
一郎花子と書いたところが一郎クンと花子さんの出会った位置です。一郎二郎から一郎花子までは、一郎クンが4分で進むきょりだから100×4=400m。また、そのとき花子から一郎花子までは花子さんが4分で進むきょりだから、60×4=240mです。これらを合計すると400+240=640m。これは一郎二郎からそのとき花子までのきょりです。
もう少しで終わります。あとちょっとがんばってください。
2つめの図で一郎二郎からそのとき花子までのきょりが640mとわかりました。それをふまえて最初の図に戻ってみましょう。
一郎二郎からそのとき花子までの640mとは、同じ地点から同じ方向に進んだ二郎クンと花子さんの差になっています。二郎クンと花子さんの分速の差は80-60=20m。つまり、二郎クンと花子さんが1分ずつ歩けば2人の差は20mになります。(二郎クンが20mリードする)
それが640mの差になっているということは、640÷20=32より、最初の図は出発してから32分後の図だったのです。
いよいよラストの式です。
一郎クンと二郎クンが反対方向に回って32分で出会ったことから、2人が32分で進んだきょりを合計して、
100×32+80×32=(100+80)×32=5760m
これが問題の池のまわりの長さです。解決!!!
***
池のまわりを3人が回る旅人算を理解していただけたでしょうか? わからなかったら何度か読み直してくださいね。
そのとき花子!を3人のまるい旅人算の合い言葉として忘れないでください。
それではまた次回の講座でお会いいたしましょう。
 NEWみんなの算数講座への質問やご意見、筆者ウタマル先生へのお便りは、メールのイラストをクリックして、メールフォームからお寄せください。
NEWみんなの算数講座への質問やご意見、筆者ウタマル先生へのお便りは、メールのイラストをクリックして、メールフォームからお寄せください。













