Newみんなの算数講座25 山縮め法

みなさんこんにちは。今回の講座25では、僕が山縮め法(やまちぢめほう)という名まえをつけた速さの問題のユニークな解き方を紹介します。どんなに長い山道でも１kmに縮めてしまう…　覚えておくと使えるときがくると思いますよ。

では問題を出しますね。

この問題にはよく使われる解き方があります。それは今回のテーマの山縮め法ではなく、比を使って解く解き方です。こっちで教える先生の方が多いと思うので、まずは比を使う解法を解説しておきますね。

比を使う解法
＊解説文中の分数の表記は分子/分母です。帯分数の整数部分と分数部分は別カラーで表示します。
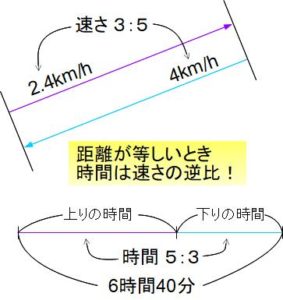
同じ距離を進むとき、速さの比と所要時間の比は逆比になります。
行きと帰りの速さの比は 2.4：４＝24：40＝３：５だから、
行きと帰りの所要時間の比は５：３(逆比)です。
合計の所要時間６時間40分を５：３に比例配分して、行きか帰りの所要時間を求めます。(どちらかを求めれば答えが出せます)

では帰り(下り)の所要時間を求めましょう。
往復にかかった６時間40分を分数で表すと６と２/３(時間)です。これを５：３に分けた３のほうが帰り(下り)の所要時間です。

帰り(下り)の所要時間
＝６と２/３(時間)×３/(５＋３)＝６と２/３(時間)×３/８＝５/２(時間)
＊行き(上り)の所要時間なら６と２/３(時間)×５/８＝25/６(時間)

あとは速さ×時間で距離を求めます。
ふもとから頂上までの距離は時速４kmで５/２(時間)かかるから、
４×５/２＝10ｋｍ　これが答えです。

比を習っていればとても自然な考え方ですね。僕もこの解き方で教えることも多いですけど、やはり算数は頭の引き出しが広い方が他の問題への対応力が増しますからね。算数のレベルアップのために、次に解説する山縮め法についても頭に残してほしいと思います。

ではやってみます。
①ふもとから頂上までの距離を１ｋｍとすると、往復の所要時間は、
(１÷2.4)＋(１÷４)＝５/12(時間)＋１/４(時間)＝２/３(時間)

メモ　１÷2.4は10÷24と同じです。10/24を約分して５/12になります。

②実際の往復所要時間は６と２/３(時間)だから、これが①で求めた１kmの往復所要時間の何倍になっているかを計算します。
６と２/３÷２/３＝20/３÷２/３＝10(倍)

山を１kmと考えたときの往復に比べ、実際の往復には10倍の時間がかかっているから、ふもとから頂上までの距離は仮定した１ｋｍの10倍です。つまり10ｋｍですね。

いかがでしたか？最初の比の解き方のほうが頭になじむ人が多いかもしれませんね。僕が教えてきた歴史の中でもそうでした。
１ｋｍを往復する時間を何倍すれば実際の往復時間になっているのか？その倍率こそが実際の山の距離だろう！という山縮め法はとても算数らしい柔らかい発想なのですが、僕の経験ではこの山縮めの発想ができる人はホント少ないです。「そうではないことをムリヤリそうする考え方」ってどこかウソをつくような気持があって受け入れにくいのでしょうね。比の解き方で満足する生徒が多いから教える先生が少ないというのもあるでしょうね。

今日この講座を読んでくれたみなさんは大丈夫ですね。山縮め法という妙な名まえを目にしただけで、簡単には忘れない思い出になったのではないかと思います。前にも書きましたが算数はインパクト(印象深さ)がすごく大事なんですよ。人間、薄い印象はすぐに忘れてしまうからです。だからみなさんの記憶に長く残る名まえをこれからもたくさん考えて発表しますよ。塾とか世間では通じなくても、みなさんが算数をやるときに活かしてくれたら僕は大満足です(*^^)

では今回はここまでにしますね。また次の講座でみなさんに算数の話ができることを楽しみにしています。