Newみんなの算数講座34 取り違え算

みん算からニューみん算への大改訂作業。むかし書いた講座はどうもムダな雑談が多くて、改めて読んでみると自分で書いたことが自分でおかしくなってしまうときがありますね。世界にふたつとない歴史に残る読みやすい算数講座にリニューアルしたいので(大げさ？ 笑)気合いを入れて完走を目指します。102講座ぶんの34講座。約分して３ぶんの１まできましたよ。自分頑張れ～(*^^)

講座34のテーマは取り違え算にしました。取り違え算は差集め算の一部に分類されることが多いですが、僕としては独立した名まえを用意してあげてもいいな～と思う個性的な文章題です。なのでこの講座は取り違え算というタイトルにしました。

さっそく問題を出しましょう。これが取り違え算です。

ｘ ｙの連立方程式が使えるなら早そうですけどね。でも算数ですから方程式は禁止です。講座28でも書きましたが、算数は方程式禁止のハンデをアイデアで克服する勉強なんですよ。そのために頭を使うことが算数の生命線だから、方程式のことは原則忘れてくださいね。(じつはマルイチ算という方程式もどきがあるんですけどね。それについてはいつか書きますね)

では解説します。取り違え算は次のような図(メモ?)を書くのが一番わかりやすいと思います。面積図ではないし。線分図とも言えませんね。僕の授業ではこのような図を様子図と呼んでいます。様子がわかるように書いているからですね。(正式な言葉ではないですよ。念のため)

最初に考えておきたいことは、買う個数を取り違えてお金が余ったということは、当初の予定では〈うなぎおにぎり〉を多く買うつもりでいたのに、実際には〈しゃけおにぎり〉を多く買ってしまったということです。もしこれが逆の間違い(しゃけを多く買う予定がうなぎを多く買った)なら、お金は余るのではなく足りなくなってしまうはずですね。

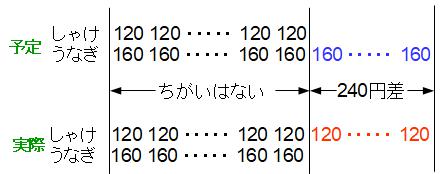
予定の買い方も実際の買い方も、黒い数字の部分にはちがいはないから、合計の値段のちがいの240円は右側に飛び出している部分(青い数字と赤い数字)で生じたことになります。うなぎ(青い金額)としゃけ(赤い金額)の値段の差は１個ずつなら160－120＝40円なので、240円の差が生じたということは240÷40＝６より、右側に飛び出ている個数が６個とわかります。この６個がしゃけとうなぎの個数の差です。(うなぎを６個多く買う予定だった)

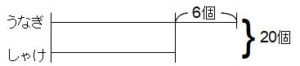
差が６個とわかったから、あとは合計20個の条件と合わせれば下の線分図のような簡単な和差算になります。
(20＋６)÷２＝13個 →予定していたうなぎおにぎりの個数
20－13＝７個 →予定していたしゃけおにぎりの個数

取り違え算、簡単だったでしょうか。
この問題でよくある間違いは、求める個数を取り違えてしまうことですね。取り違え算の答えを取り違えたらシャレにならないですね～(笑) 予定ではどちらを多く買ってどちらを少なく買うつもりだったのか？という判断が大事です。合計の代金が〔予定＜実際〕なら安い方を多く買うつもりだったし、〔予定＞実際〕なら高い方を多く買うつもりだったということです。そこをミスしなければ取り違え算は難しい問題ではないですね。

難しい講座ばかりではみなさんが疲れてしまうでしょうし。簡単な講座ばかりでは退屈だしわざわざ読んでもらう意味もないですよね。難易がかたよらないようにバランスを考えながらこれからも書いていこうと思います。難しくてもあきらめないでくださいね。簡単だったらホッとしてください。
では講座34講座はこれで終わります。みなさん次の講座までお元気で！