NEWみんなの算数講座105 時計算の二歩目

みなさんこんにちは。NEWみんなの算数講座105回目です。

103回目の背番号問題の解説は、話が長引きそうなので、この講座とは別に臨時号として投稿します。この講座には書きませんのでご了承ください。

今回は久しぶりに時計算を解説しようと思います。64回目の「時計算の初歩」以来ですね。タイトルはその続きという意味で「時計算の二歩目」にしました。やや応用的な内容です。時計算を基本から～という人は、先に64回をお読みになってください。また、43回でも時計算にふれたことがあります。そのときはシャドー針というマニアックな解法の紹介でした。シャドー針は、その発想をすることが易しくないので、今回は持ち出さずに解説することにします。

では１問目です。長針と短針が左右対称になる時刻を求めます。

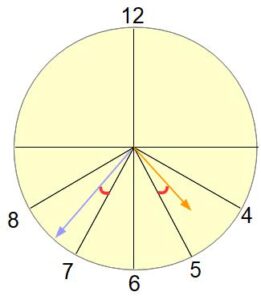
初歩のときにも書きましたが、こうした時計算の問題は、与えられた始まりの時刻（この場合は４時）に戻した状態を書き入れてみることが大切です。そのことによってだいぶ様子が見えてくるのです。

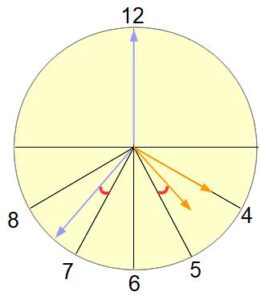
４時を書き入れてみました。
あとはこの図の中で、長針と短針が動いた角度を調べ、式が作れる状態に持ち込むことを考えましょう。

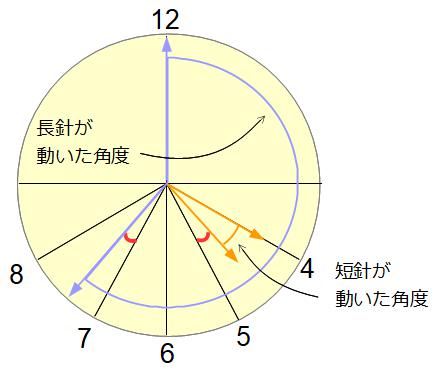
図の中に、長針が動いた角度と短針が動いた角度を示しました。もちろん「４時から、求める時刻になるまでに動いた角度」です。
この状態では、まだ式を作ることができませんが、何か気づきませんか？

気づいた人もいると思います。短針が動いた角度を「右から左に移す」ことができますね。下の図のようになります。

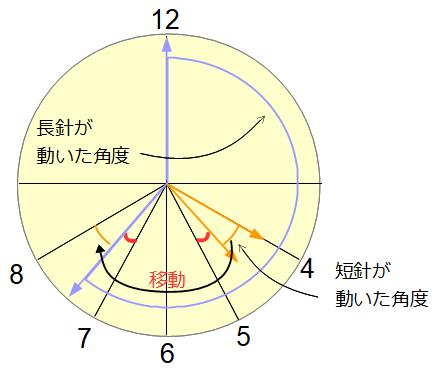
この移動によって、長針と短針の動いた角度が、合計でちょうど文字盤の８マス分になっています。文字盤１マスは30°なので、８マスだと240°です。

ということで、「長針と短針が合計で240°動くのにかかる時間」←これを求めれば、この問題の解答になります。
長針は１分間に６°、短針は１分間に0.5°でした。合計すると6.5°で、長針と短針は１分間に合わせて6.5°進みます。それが何分たてば240°になるか？
割り算で求めることができますね。
240÷6.5＝240/6.5
分母と分子を２倍して480/13分、帯分数に直して36と12/13分。
求める解答は４時36と12/13分です。

ではもう一問いきましょう。時間の経過で長針と短針が入れ替わるという有名な問題ですが、(2)がややこしいと思います。

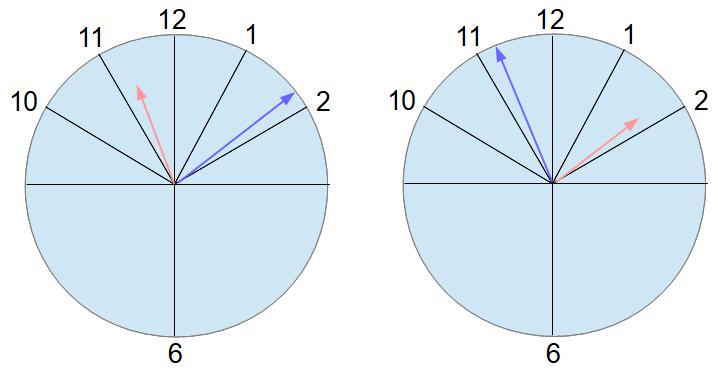
(1)は１問目の問題と似ています。家を出た時刻から、帰ってきた時刻まで、長針と短針がどのように動いたかを考えます。
短針は見たままで、左の図の位置から右の図の位置までが動いた角度です。
長針は、正午に「12」の位置に戻り、午後１時に再び「12」の位置に戻り、その後、右の図の位置まで動いています。つまり長針は、文字盤の３周に「左右の図の両針のへだたり」だけ足りない角度を動いたということです。図にしてみましょう。

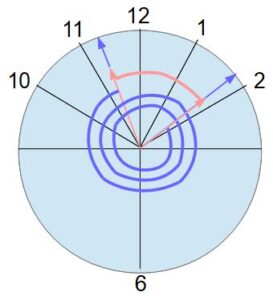
この図を作るのは正直苦戦しました(汗)なんとか読み取ってもらえることを期待します。
長針が３周弱回っていて、それに短針が回った角度をたすと、ちょうど文字盤の３周分になります。１周360°だから３周は1080°です。長針と短針が動く角度の合計は１分で６＋0.5＝6.5°だから、あわせて1080°動くのにかかる時間は、
1080÷6.5＝1080/6.5＝2160/13＝166と２/13分＝２時間46と２/13分です。これが千代さんが買い物に出かけていた時間です。

(2)がややこしいです。しっかり読んでください。
左の図から右の図までに両方の針が動いた角度の合計は1080°でした。この1080°を長針が動いた角度と、短針が動いた角度に分けてみます。
長針と短針が同じ時間で動く角度の比は、１分あたりに動く角度の比を使って、６：0.5＝12：１です。
つまり、1080°のうち、長針が動いた分が12/13、短針が動いた分が１/13です。1080°のうち、短針が動いた角度は1080/13°です。この1080/13°が問題の図の両方の針のへだたりです。
[くわしく]
短針は、左の図のピンクの位置から、右の図のピンクの位置まで動きました。右の図のピンクの位置は、左の図のブルーの位置なので、短針が動いた角度は、図の両方の針のへだたりです。

右の図を見てください。このとき両方の針のへだたりは1080/13°ですが、まもなく午後２時です。午後２時には両方の針のへだたりは60°になります。
＊２時を思い浮かべてみてください。２時は60°ですよね？

・右の図の時点　➡　両方の針のへだたりは1080/13°
・午後２時になると　➡　両方の針のへだたりは60°

1080/13°差が60°差になるまで長針が短針を追いかけていくと、長針は短針より１分あたり６－0.5＝5.5°多く進むから、1080/13°差が60°差になるまでにかかる時間は、
（1080/13－60）÷（６－0.5）＝（1080/13－780/13）÷5.5
＝300/13÷11/２＝300/13×２/11＝600/143分＝４と28/143分です。

右の図の時刻は、午後２時になる４と28/143分前というわけですね。千代さんが買い物から戻ってきた時刻は、２時－４と28/143分＝午後１時55と115/143分です。

以上で解決しました。６＋0.5＝6.5°が出てきたり、６－0.5＝5.5°が出てきたり、やさしい問題ではないですね。一度で自信がない人は、何度か読み直してくださいね。きっと理解してもらえると思います。しかしそれにしても時計算はすごい答えになりますね。算数の文章題で分母が143なんて答えが出てくるのは時計算ぐらいです。でもそれが時計算の個性なんですよね。

＊＊＊
今回も読んでもらってありがとうございました。次は103回目の背番号問題の解答をはさみまして、106回目から何回かにわたり、１回目の講座に戻って復習テスト編を作る予定です。この講座の初期は、読者のみなさんに宿題を出して、コメントらんで解答を受けていたのですが、その後コメントらんを閉じた経緯があり、初期の講座の説明を直すために企画しました。どういう形の復習テスト編になるか、楽しみに待っていてくださいね。それでは今回はここまでにします。

余談　このサイトはwordpressという圧倒的ユーザー数のweb製作ソフトで作ってます。とても優れモノですが、デフォルトのコメントらんを置くと、スパムなどの自動コメントが大量です。ここにも日に数十個毎日でした(汗) wordpressのアキレス腱でしょうかね。そのため、現在はコメントらんを閉じて、外部フォームを使っています。

インフォメーションボード

〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。

〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。

〈算数講座へのご意見や質問／ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。

〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、５講座ずつを１冊子にまとめ、「なかとじ印刷」した片側Ａ５サイズ（開くとＡ４）のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら