NEWみんなの算数講座104 プリン

みなさんこんにちは。NEWみんなの算数講座104回目です。
 今回は、立体図形のジャンルから、円すいから円すいを切り取った円すい台についてお話ししようと思います。形状が似ていて説明が早いので、僕は何年もプリン、プリンと呼んでいますが、改めて写真で探してみたら、やっぱりプリンですね。いつも僕がつける名前は、ここだけのオリジナルが多いけど、これはきっと日本じゅうの算数の先生の呼び方がプリンかもしれませんね。今回の講座タイトルもプリンにしました(笑)
今回は、立体図形のジャンルから、円すいから円すいを切り取った円すい台についてお話ししようと思います。形状が似ていて説明が早いので、僕は何年もプリン、プリンと呼んでいますが、改めて写真で探してみたら、やっぱりプリンですね。いつも僕がつける名前は、ここだけのオリジナルが多いけど、これはきっと日本じゅうの算数の先生の呼び方がプリンかもしれませんね。今回の講座タイトルもプリンにしました(笑)
ではさっそく問題を出してみようと思います。求めるものはシンプルに、体積と表面積です。
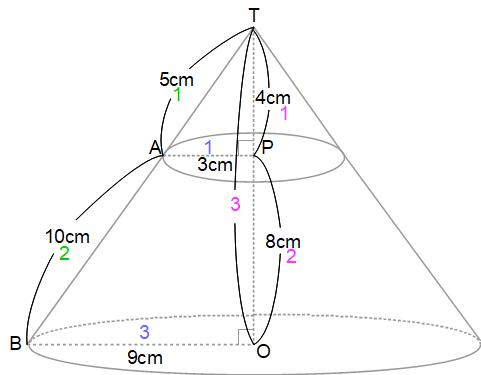
下の図の円すい台について、次のものを求めてください。円周率は3.14とします。
(1)体積
(2)表面積
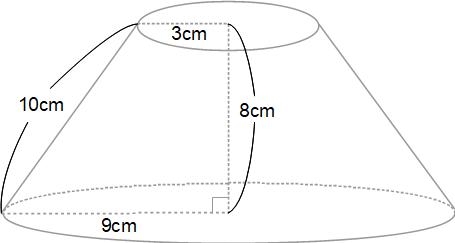
均一な線で書いていて、保存するまでは違和感ないのですが、webに置くと線の細い箇所ができてしまいます。どうしてだろう?web図版は難しいですね。そこは素人なので大目にみてください。
さて解説。
円すい台は、円すいから円すいを切り取った立体なので、切り取られた部分を再現する必要があります。その図版を下に用意しました。みなさんもプリン(円すい台)の問題が出たら、上部の円すいは手書きで書き加えてくださいね。
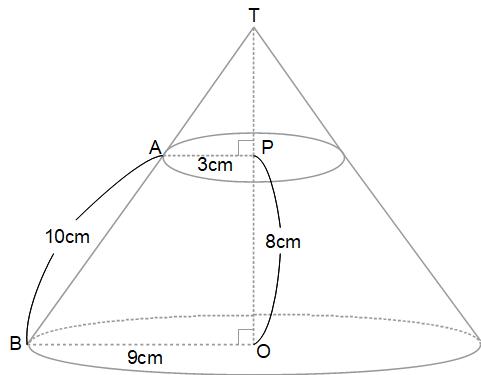
(1)
体積を求めるには2つの方法が考えられます。1つは、つけ加えた部分もふくめた大きな円すいから、つけ加えた部分の小さな円すいを引く方法。もう1つは、相似形の体積比という考え方を使って、大小どちらかの円すいの体積から、円すい台の体積を比率で求める方法です。両方解説しますね。
〈大きな円すいから小さな円すいを引く〉
この方法を使うためには、長さの情報がひとつ足りません。小さな円すいの高さ、上の図のTPです。TPの長さは、三角形の相似を使って求めます。
△TAPと△TBOは相似です。理由は「2つの角が等しい三角形は相似」という相似条件です。この場合、直角をふくめて2つの角が等しいことはすぐにわかりますね。たとえば、角TAPと角TBOは平行線の同位角です。
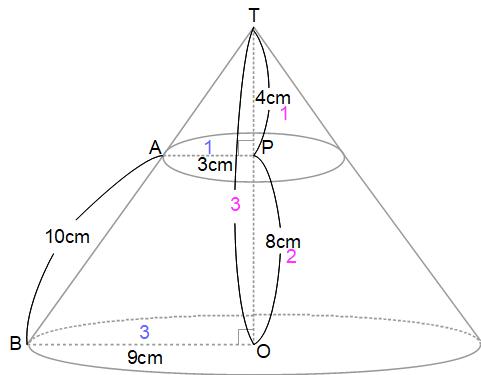
△TAPと△TBOの相似比は、半径の比から3:9=1:3です。すると高さのTP:TOも1:3になり、その差の2にあたる長さが円すい台の高さの8cmだから、1にあたる長さ、つまり小さな円すいの高さは4cmです。
これで長さの条件が出そろい、大きな円すいの体積から小さな円すいの体積を引くことができます。円すいの体積を求める公式は【底面積×高さ×1/3】です。
では計算します。
9×9×3.14×12×1/3-3×3×3.14×4×1/3
=324×3.14-12×3.14=(324-12)×3.14
=312×3.14=979.68(cm3)
これが求めるプリンの体積です。
〈相似な立体の体積比を使う〉
△TAPと△TBOが相似であることと同じように、小さな円すいと大きな円すいも相似です。小さな円すいと大きな円すいは、底面の半径、高さ、母線の長さの比がすべて1:3です。小さな円すいを3倍に拡大したものが大きな円すいです。相似というのは平面図形だけではなく、立体図形にもあるのです。
そして、相似な立体の体積比は、相似比の3乗になります。相似な図形(算数では主に三角形)の面積比は相似比の2乗でしたが、体積の場合は3乗です。体積を求めるときは、たて×横×高さのように3つの長さをかけるからですね。
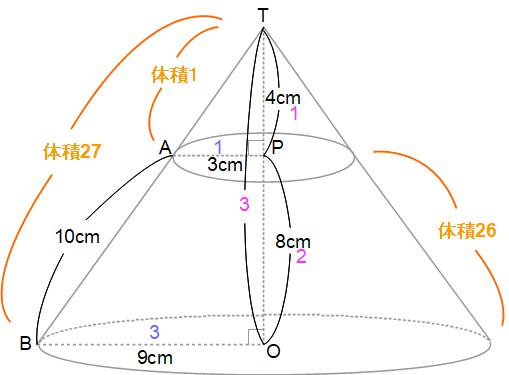
小さな円すいと大きな円すいの相似比(長さの比のこと)は1:3だから、体積の比は(1×1×1):(3×3×3)=1:27です。
*1は何回かけても1ですが、相似比の片方がいつも1とは限りません。体積比の3乗(3回かける)を忘れないでください。
すると27から1を引いてプリンの比率は26。小さな円すいの体積を26倍すればプリンの体積ということです。大きな円すいの体積にはふれずに、プリンの体積が出ます。最初に書く式も短くて、数も小さめなので、この考え方も僕としてはけっこうおすすめです。
3×3×3.14×4×1/3×26=312×3.14=979.68(cm3)
(2)
続いて表面積です。
表面積を円すい全体で考えるときについては、72回の「円すいマニュアル」をお読みください。
プリンの表面積は、上円と下円、それとまわりの側面です。まわりの側面は、円すいの側面の一部です。これも体積と同じように、大きな円すいの側面積から、小さな円すいの側面積を引けばOKです。
[上円と下円]3×3×3.14+9×9×3.14=(9+81)×3.14=90×3.14=282.6(cm2)…ア [側面]円すいの側面積の公式は【母線×底面の半径×3.14】です。大きな円すいの表面積から、小さな円すいの表面積を引きます。小さな円すいの母線は5cm(これも三角形の相似から求めます)、大きな円すいの母線は15cmです。
15×9×3.14-5×3×3.14=(135-15)×3.14
=120×3.14=376.8(cm2)…イ
*小円すいと大円すいの側面積の比は、相似比の2乗で(1×1):(3×3)=1:9になります。するとプリンの側面積は8にあたるので、小円すいの側面積を8倍して求めることもできます。体積とは違い、面積は2乗なので注意してください。
アとイを合計してプリンの表面積です。
282.6+376.8=659.4(cm2)
以上で問題は解決しましたが、ちょっと裏ワザも紹介しましょうか。
プリンの側面積は、(上半径+下半径)×母線差に3.14をかければ求めることができます。いまの問題では(3+9)×10×3.14=120×3.14ですね。これも便利なのでぜひ記憶の片隅に。かけるのは高さの差ではなく、母線の差なので、そこだけ気をつけてください。
***
今回のプリンの講座、理解していただけたでしょうか。今回のようにダイレクトに出てくるプリンの問題もありますし、軸のまわりを台形が回転してできる回転体としてもプリンは現れます。算数のテストにはよく出てくる問題なので、いつでも解けるようにしておいてほしいです。
では今回の講座はこれで終わりにします。次回もまた、みなさんの役に立つ算数を書こうと思います。どうぞみなさん楽しみに待っていてください。それではまた~!
インフォメーションボード
〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。
〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。
〈算数講座へのご意見や質問/ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。
〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、5講座ずつを1冊子にまとめ、「なかとじ印刷」した片側A5サイズ(開くとA4)のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら











