Newみんなの算数講座63 てんびんの弱点

みなさんこんにちは。ニューみん算講座63を始めます。

今回は食塩水の問題の中で、講座３で説明した〈てんびん〉だけでは解決できない問題、てんびんがまるで役に立たない問題を紹介します。てんびんは食塩水問題の強力ツールではありますが、万能ではないです。僕の経験では、てんびんだけで機械的に解決できる食塩水の問題は五割～六割。それ以外の問題では、部分的にてんびんが使えることはあっても、食塩水が変化する様子を正しくしっかりと捉えることが大事ですね。

ではさっそくそんな問題を出してみます。１番はてんびんだけでは足りない問題、２番はてんびんを使う余地がない問題です。

残念ながらこの問題は、機械的にてんびんに任せるだけでは解決しません。てんびんに加え、食塩水を交換するときの大切な見方を理解してください。
下の図を見てください。

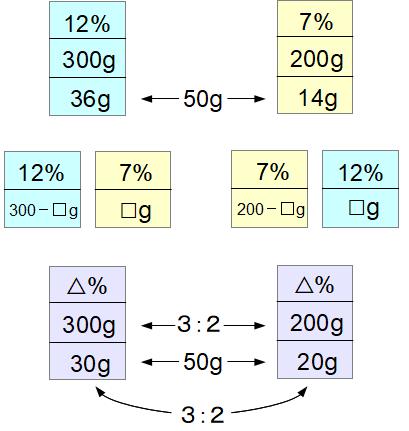
ボックス内の数値は、上段が濃度(%)、２段目が食塩水の重さ(g)、３段目があるときは食塩の重さ(g)を表しています。また、同じ濃度の食塩水を同じカラーで表示しています。

食塩水ＡとＢからそれぞれ□ｇの食塩水を反対側に移します。どちらの食塩水も□ｇ渡して□ｇ受け取るから、交換後の食塩水の重さは初めの食塩水の重さと同じになります。その結果両方の食塩水の濃度が等しくなるわけですが、このとき少し浮かびにくいのですが次のポイントがとても重要です。

その１、その２どちらを使っても最終的な食塩水の濃度を求めることができます。ここではその１を使います。
交換後の食塩水Ａは300ｇ、食塩水Ｂは200ｇです。この比率は３：２ですが、この比率と同じ比率で食塩が溶けていないと、２つの食塩水の濃度は同じになりません。ボックスに示したように食塩の総量は初めの状態の計算から36＋14＝50gです。この総量が変わることはないから(全体としての食塩は増えも減りもしていない)、交換後のＡ、Ｂに溶けている食塩は50ｇを３：２に配分した30ｇと20ｇです。食塩水Ａで計算して、交換後の濃度は30÷300＝0.1＝10％です。(ボックスの△％は10％)
＊その２も調べてみてください。初めの状態でＡとＢを混ぜても10％の食塩水になりますよ？

ここまでくればあとはてんびんに任せて大丈夫そうです。12％の食塩水と７％の食塩水を混ぜて10％の食塩水が300gできるというてんびんですね。上の図でブルーとクリーム色を混ぜて紫色になるところです。左右どちらの混合に注目してもかまいませんが僕は左の混合でてんびんを書きました。

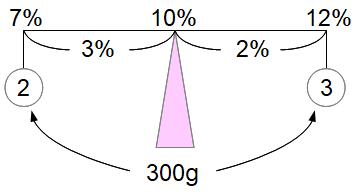
てんびんはこんな感じになりますね。７％の食塩水300×2/5＝120ｇと12％の食塩水300×3/5＝180gを混ぜると10％の食塩水が300gできます。求める□gは７％の方の120gですね。つまりＡの容器に12％の食塩水を300－120＝180g残し、そこにＢの容器からやってきた７％の食塩水120gを加えると、Ａの容器に10％の食塩水が300gできるということです。
＊このてんびんは容器Ａで10％の食塩水300gができることに注目しました。容器Ｂで10％の食塩水200gができることに注目しても同じように解けます。
＊てんびんについては講座３でくわしく解説しています。

問題１はてんびんも使いましたが、次の問題２ではてんびんが使える余地はないです。ではその問題２です。

この問題は、例年悩んで迷路に入り込んでしまう生徒がたくさんいます。食塩水を混ぜるわけではないから〈てんびん〉を使う余地はありません。みなさんは冷静に対処できますか？

坂本君が間違えて作った食塩水と、作り直した正しい食塩水を比べます。
【Ｍ　間違いの食塩水】
食塩15ｇ　水100ｇ　食塩水115ｇ　濃度15/115＝3/23

【Ｒ　正しい食塩水】
食塩15ｇ　水85ｇ　食塩水100ｇ　濃度15/100＝15％

Ｍの食塩水をＲの食塩水に直したいわけですが、食塩水を15ｇ減らすとは考えずに、水を15ｇ減らすと考えてください。
Ｍの食塩水の濃度は3/23だから、水の占める割合は１－3/23＝20/23
よって、Ｍの食塩水が水を15g含むための食塩水の量は、□ｇ×20/23＝15ｇを逆算して15÷20/23＝17.25g
つまり、Ｍの状態から食塩水17.25ｇを捨てれば水を15ｇ減らすことができます。

ところが
このことで水を15ｇを減らすことはできますが、食塩水17.25ｇの中には17.25×3/23＝2.25ｇの食塩が含まれていて、それも同時に捨てられてしまうから、その分の食塩を補わなくてはなりません。よって、あとでとかした食塩の量は 2.25ｇです。
＊17.25－15＝2.25ｇでもかまいません。

問題２の解答　捨てる食塩水17.25ｇ　あとでとかした食塩2.25ｇ

以上、食塩水の問題にはてんびんだけでは解き切れない問題や、てんびんが関係しない問題もあるというお話でした。たくさんの塾が食塩水のてんびんをはやらせちゃったものだから、入試問題ではてんびんだけでは済まない問題も半分はありますね。ほとんどのテキストや問題集に食塩水だけのページがあると思いますから、今回の講座のような問題を見つけて練習を積んでくださいね。食塩水問題ならなんでもまかせろ！そんな頼もしい人がいっぱい現れることに期待したいと思います。
それでは今回の講座63を終了します。次回の講座64は元祖のボツ(廃止)が決定しています。何が飛び出すでしょうか？どうぞお楽しみに～！

カーテンコール
問題１で容器Ａに最初に溶けている食塩は36g、交換後に溶けている食塩は30gです。６ｇの食塩が減少してますね。もちろん容器Ｂでは６ｇ増えています。このことに注目し、てんびんを用いない解法もあります。もしＡＢの相互交換が１ｇだったら容器Ａでは１g×0.12－１g×0.07＝0.05ｇの食塩が減るはずです。実際の減少は６ｇだから６÷0.05＝120ｇの交換だったわけですね。え？こっちの方が早くてラク？ そうかもしれませんね。算数はいろいろな引き出しが持てるから楽しいのです(^^)/ 講座25の山縮め法がこの考え方と似てますね。ぜひどうぞ！