Newみんなの算数講座31 N角形の公式集

算数ファンのみなさんこんにちは。
今回は平面図形のジャンルからN角形の公式集です。中学受験で使うのは〈N角形の内角の和〉〈N角形の外角の和〉〈正N角形の1つの内角の大きさ〉〈N角形の対角線の本数〉といったところでしょう。これらを覚えていないとさすがに図形の問題は戦えないですよ。
それではまずN角形の公式を紹介します。どれもしっかり頭にたたきこんでくださいね。公式の理由はあとで説明します。
| 求めるもの | 公式 |
| N角形の内角の和 | 180×(N-2)° …A |
| N角形の外角の和 | 360° *一定値 |
| 正N角形の1つの内角の大きさ① | (A÷N)° |
| 正N角形の1つの内角の大きさ② | (180-360÷N)° |
| N角形の対角線の本数 | (N-3)×N÷2 本 |
使い方の例
N角形というのは多角形と同じ意味ですが、公式を用意するときはN角形としますね。五角形ならN=5、六角形ならN=6のように、Nに数をあてはめて計算します。Nは数値を変えられる代表の意味です。外角の和は一定の値だから計算する必要がありません。(外角の和は三角形でも十五角形でも六十角形でも360°で変わりません)
・八角形の内角の和 180×(8-2)=180×6=1080°
・正八角形の1つの内角 1080÷8=135°
・八角形の対角線の本数 (8-3)×8÷2=5×8÷2=20本
では、いまの公式を使って計算した三角形から十二角形までの一覧表をどうぞ。この一覧表ってありそうであまりないと思います。僕は十二角形でやめましたが、がんばり屋さんの人はもう少し下まで作ってみてください。何角形まで続けたらギネスブックかな(笑)
| 内角の和 | 外角の和 | 正N角形の 1つの内角 |
対角線 | |
| 三角形 | 180° | 360° | 60° | 0本 |
| 四角形 | 360° | 360° | 90° | 2本 |
| 五角形 | 540° | 360° | 108° | 5本 |
| 六角形 | 720° | 360° | 120° | 9本 |
| 七角形 | 900° | 360° | 128と4/7° | 14本 |
| 八角形 | 1080° | 360° | 135° | 20本 |
| 九角形 | 1260° | 360° | 140° | 27本 |
| 十角形 | 1440° | 360° | 144° | 35本 |
| 十一角形 | 1620° | 360° | 147と3/11° | 44本 |
| 十二角形 | 1800° | 360° | 150° | 54本 |
さて大事なのは公式たちの理由ですね。「公式だから」は理由にならないですよ。それぞれちゃんと理由があります。では順番に説明していきますね。
内角の和について
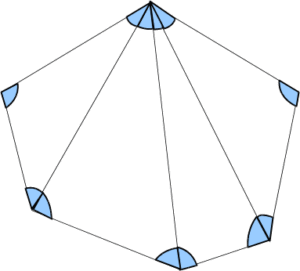
下の図は六角形を4つの三角形に分割した様子ですが、このようにN角形は必ずN-2(個)の三角形に分割することができます。三角形の内角の和は180°だから、N角形の内角の和は180×(N-2)°になります。
外角の和について
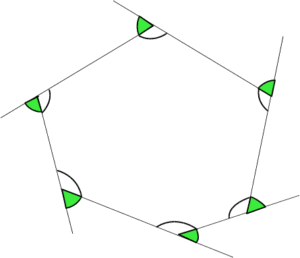
外角というのは、内角を180°に延長した外側の角(緑色の角)を指します。下の図の六角形の場合、6つの頂点に6本の直線があり、合計すると180×6=1080°です。ここから六角形の内角の和720°(白い角の合計)を引くと1080°-720°で外角の和は360°になります。
N角形の場合でも、180×N-180×(N-2)という式ができて、この式はNコの180°から、Nより2コ少ない180°を引いているから、180°が2コ残って360°になります。このように外角の和は何角形に関係なく必ず360°です。
正N角形の1つの内角の大きさについて
ふたつの方法が使われます。
①正N角形はすべての角の大きさが等しいN角形だから、内角の和180×(N-2)°をNで割ればよいです。
②外角の和(360°)をNで割って1つの外角を先に求め、それを直線の180°から引くという方法もあります。問題の内容によってはこの〈第二公式〉の方が便利なことがあります。
対角線の本数について
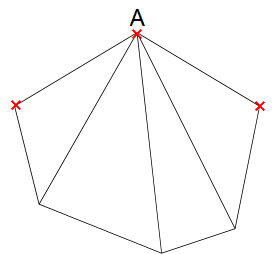
下の図の六角形で、1つの頂点Aに集まる対角線は3本です。頂点Aから両隣りの頂点と自分自身の3つの頂点は対角線が引けません(×印)。N角形は1つの頂点にN-3(本)の対角線が集まっていて、これに頂点の数Nをかけると(N-3)×N ただしこのままだと往復する対角線をダブッて数えているから、N角形の対角線の本数は(N-3)×N÷2(本)です。
以上N角形の公式とその理由でした。内角の和は180°ずつ増えますし、対角線の本数は2、3、4、5、…と増えていくなどきれいな法則もあります。六角形ぐらいまでは公式不要かもしれないです。ただ、Nの値が大きいときもありますから、やはり今回の公式は暗記しなくてはいけませんね。と言っても外角の和は一定値だし、「1つの内角①」は内角の和をNで割るだけですから、暗記といっても3つの式だけです。他の教科に比べたら覚えることはそれほど多くない算数ですが、今回の式はスーパー重要ですから絶対に忘れないでください。
では今回の講座はこれにて終了しますね。次の講座はなるべく早めに書きます。楽しみに待っていてください。
みなさんへの宿題
正N角形の1つの内角の大きさを考えると、正三角形60°、正四角形(正方形)90°、正五角形108°のように整数になる場合もありますが、正七角形、正十一角形などのように整数にならない場合もあります。Nを3以上30以下の整数としたとき、1つの内角の大きさが整数になる場合は何通りありますか?
解答したい方はページ下のコメントに書いてください。正解不正解をレスさせていただきます。お名前はニックネームでもかまいません。













