Newみんなの算数講座68 数表シリーズ③奇数和

みなさんこんにちは。ニューみん算講座68です。

今回は講座44の三角数、講座47の平方数に続いて３回目の数表問題です。数表の中で必ず成り立つ不変の規則を発見することができれば、どんなに遠い場所を聞かれても、きまった手順で対応できるのが数表問題の楽しいところですよね。
ということはいかに揺るぎない規則を発見できるかどうかがポイントになりますね。ではさっそく問題にいってみましょう。役に立つ公式も出てきますからしっかり読んでくださいね。

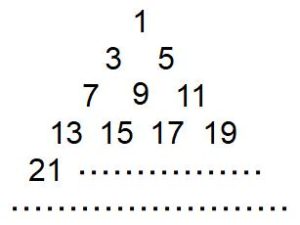
１段目に１個、２段目に２個、３段目に３個、……のように奇数だけがピラミッド状に並べられています。

(1)
各段の左端の数だけを抜き出すと次のような階差数列という数列になります。赤い丸数字はこの数列の項に付けた番号、ブルーの数は項と項の間隔です。

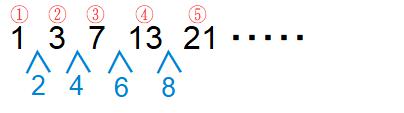
この数列は項と項の間隔が
２　４　６　８　・・・・・のように偶数の数列になっています。間隔が階段状に増えていくから階差数列といいます。
たとえばこの数列の⑤番目の数を求めるには、項と項の間の偶数(ブルーの数)を２から順に４個加え、それを先頭の項の１にたせばよいですね。
⑤＝(２＋４＋６＋８)＋１＝20＋１＝21 です。

⑧番目の数も同様です。項と項の間の偶数を２から順に７個加え、それを先頭の項の１にたします。
⑧＝(２＋４＋６＋８＋10＋12＋14)＋１
＝｛ (２＋14)×７÷２｝＋１
＝56＋１＝57

メモａ
間にある偶数の個数は、⑤番目なら４個、⑧番目なら７個というように項より１個少なくなります。これは「指が５本あるとき指と指の間隔は４ケ所」という植木算の考え方です。

メモｂ
２から数えて□個目の偶数は単純に２×□で大丈夫です。４個目の偶数は２×４＝８、７個目の偶数は２×７＝14です。

メモｃ
２＋４＋６＋８＋10＋12＋14 ＝ (２＋14)×７÷２
この計算は等差数列の和を求める計算です。
等差数列の和＝(初めの数＋終わりの数)×項数÷２ です。

(2)
まず、(1)と同じように25段目の左端の数を求めます。さきほどの数列の25番目です。

項と項の間の最後の偶数は２×(25－１)＝48です。
上のメモｃの公式を使って、
〇25＝(２＋４＋………＋46＋48)＋１
＝｛ (２＋48)×24÷２｝＋１
＝600＋１＝601
25段目の左端の数を601と求めることができました。

25段目には25個の奇数が並んでいます。その25個の奇数の中央の数は左から数えて13番目の数です。左から13番目の数は、左端の601に２を12回たせばよいから(13回ではない！)
求める解答は601＋２×(13－１)＝601＋24＝625です。

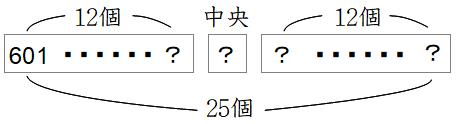
メモｄ
じつは〈奇数段目の中央の数＝段数×段数〉という規則もあります。この場合は25×25＝625です。気づいた人もいるでしょうか？

(3)
ここまでは設問(1)を用意した都合上、左端の数を手がかりにしましたが、この数表では次のように並んでいる奇数自体をナンバリングして考える方法も有力だと思います。(3)はこちらで考えてみます。

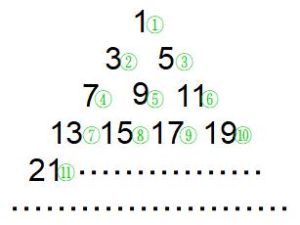
このナンバリングでは〈〇番号×２－１〉で奇数が特定されます。一例は⑧＝８×２－１＝15などです。
１段目に１個、２段目に２個、３段目に３個、……のように奇数が並ぶから、99段目には99個の奇数が並び、１段目から99段目までの奇数の総個数は
１＋２＋３＋……＋97＋98＋99
＝(１＋99)×99÷２
＝100×99÷２
＝4950より、4950個とわかります。

100段目はその次の段だから、〇番号4951番から100個の奇数が並び、最後の奇数の番号は4951＋100－１より〇番号5050番です。(１段目から100段目までの奇数の総個数は5050個です)
〇番号4951番と〇番号5050番の奇数を求めます。
〇番号4951番＝4951×２－１＝9901
〇番号5050番＝5050×２－１＝10099
よって100段目には9901から10099までの100個の奇数が並んでいます。

これらの和はメモｃの公式を使って、
(9901＋10099)×100÷２＝20000×100÷２＝100万
と求めることができます。

ひととおり設問の解答は出ましたが、(3)の別解をもう一つ書いておきましょう。

【(3)の別解】
次のような奇数和を求める有名な公式があります。

１から順に奇数をたした和＝たした奇数の個数×たした奇数の個数

たとえば１＋３＋５＋７は１から順に４個の奇数をたしてますよね？ これらの和を４×４＝16と求めることができるのです。もう一例調べましょうか。
１＋３＋５＋７＋９＝５×５＝25です。

このことを使って、100段目の奇数の和を「１段目から100段目のすべての奇数の和」から「１段目から99段目のすべての奇数の和」を引くという方法で求めることができます。

さきほど99段目までに4950個の奇数があり、100段目までに5050個の奇数があることを計算しましたからそれを使います。

〈１段目から100段目のすべての奇数の和 → １から順に5050個の奇数を加えた和〉
上の奇数和の公式を使って 5050×5050…ア です。

〈１段目から99段目のすべての奇数の和 → １から順に4950個の奇数を加えた和〉
4950×4950…イ です。

100段目の奇数の和はアからイを引いて 5050×5050－4950×4950 です。普通に計算はちょっと大変ですね。どう計算しましょうか。数学なら
Ａ²－Ｂ²＝(Ａ＋Ｂ)×(Ａ－Ｂ)
＝(5050＋4950)×(5050－4950)＝10000×100＝100万
という因数分解の利用ができますね。算数はこれはできないから下の図のように面積を使って近道する手を使いましょうか。

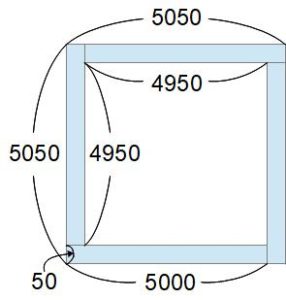
１辺5050の正方形の中央に１辺4950の正方形を書きます。その面積の差は、折り紙の風車状(ちょっとたとえが違うかな???)になっている短い辺の長さが50、長い辺の長さが5000の長方形４つ分です。
5050×5050と4950×4950の差は (50×5000)×４＝250000×４＝100万

以上講座68、数表シリーズ③でした。数表問題の解説を書いていると、次から次から別解を思いつきます。そのすべてを書くことはできませんが、数表問題にはそれだけたくさんのアプローチがあると考えてください。だから僕の解説と同じではなく、自分ならこう考えるな～ というのも全然オーケーだと思います。手と頭を動かしていろいろな法則を探してみてください。僕が触れてない名案があったらぜひコメントで知らせてくださいね。楽しみに待ってますよ。

次回は速さの文章題のスリートップの一員、通過算を取り上げます。タイトルは通過算の呪文ワワルワ、ワワルサです。なるべく早く書いて発表しますから楽しみに待っていてくださいね。では次回までごきげんよう！(*^^*)

カーテンコール
今回の講座に、１から順に奇数をすべてたす奇数和の公式が出てきましたが、２から順に偶数をすべてたす偶数和の公式もあるので書いておきますね。
２から順に偶数をたした和＝たした偶数の個数×(たした偶数の個数＋１)