Newみんなの算数講座47 数表シリーズ②平方数

みなさん今日もニューみん算へようこそ～。
今回は47講座目ですが、元祖講座の47番は残さないことにしまして、ニュー講座用に新しい講座を書くことにしました。ニューになって新しく書いた講座は23、35、36、44番に続いて５個目です。むかし書いた元祖講座はおかげさまで人気の回もたくさんありますが、量産してる中でさえない回もありました。それもふくめて僕はとても懐かしいですけどね(*´з`)
という言い訳をして新作への変更です。テーマは数表シリーズ②を持ってきました。

数表は講座44に続いて２回目です。講座44では斜めラインの終点に必ず三角数が現れる数表を取り上げましたが、おそらくあの数表と今回の数表がよく出る数表の１，２位を争うと思います。算数のテストではこの二つが抜きん出てよく出題されますね。だから講座44と今回の講座をマスターしておけば数表問題の予防接種は終わったという感じでしょうね。

ではいつものように問題を出しましょう。

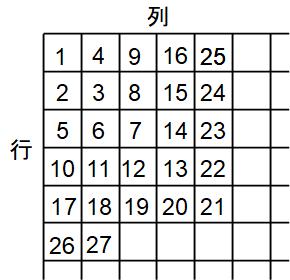
まずこの数表の特長を整理してみますね。下の図を見ながら読んでください。

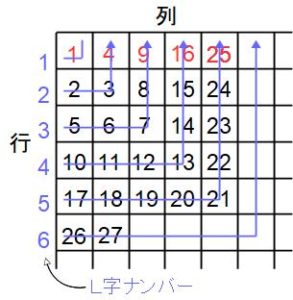
〈特長１〉青い線で示したように、１から始まる整数が下から上に向かって逆Ｌ字(以下Ｌ字と表記)を作るように収まっていきます。最初の１は単独ですが、Ｌ字が徐々に大きくなっていきますね。

〈特長２〉上から順にＬ字をナンバリングすると、どのＬ字の終点にもＬ字ナンバーを２回かけた平方数と呼ばれる数が並んでいます(平方数は赤い数字で示しました)。たとえばＬ字ナンバー５の終点は５×５＝25です。あるＬ字が終わると、次のＬ字は平方数の次の数から始まります。平方数については下の囲みも参照してください。

〈特長３〉各整数の行数か列数のどちらか(または両方)がＬ字ナンバーと一致します。
整数がＬ字の横線上にあるとき、行数とＬ字ナンバーが一致して「行数≧列数」です。
整数がＬ字のタテ線上にあるとき、列数とＬ字ナンバーが一致して「列数≧行数」です。

〈特長４〉Ｌ字のカドは行数と列数が同じで、Ｌ字の始まりの数と終わりの数の平均値になります。たとえばＬ字ナンバー５のカドにある５行５列の整数は17と25の平均で(17＋25)÷２＝21です。

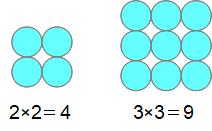
では設問を考えていきましょう。
(1)
７行９列は行数より列数の方が大きいから、〈特長３〉よりＬ字ナンバー９のタテ線上に並んでいます。〈特長２〉からＬ字ナンバー９の終点は９×９＝81です。７行目の数は１行目の数より６小さいから、正解は81－６＝75です。

(2)
21行15列は行数が列数より大きいから、〈特長３〉よりＬ字ナンバー21の横線上にあります。ひとつ前のＬ字ナンバー20の終点が20×20＝400が終点だから、Ｌ字ナンバー21は401から始まります。15列目の数は１列目の数より14大きいから、正解は401＋14＝415です。

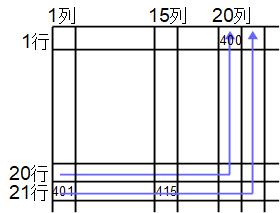
(3)
794の位置を特定するには、794に近い平方数を探すことになります。25×25＝625では足りないし、30×30＝900では大きすぎますね。この近くで平方数を調べると28×28＝784、29×29＝841です。794はこの間にありますね。
Ｌ字ナンバー28の終点が784 (28×28) だから、Ｌ字ナンバー29は785から始まります。794－785＝９より、794は１列目から右に９列進んだ10列目にあります。正解は29行10列です。
＊794－785＝９列目ではないです。数表の問題ではこうした細かい点に十分注意してください。答えが近づいてきたらすべて書いてもよいでしょう。

新作講座の数表第二弾を理解してもらえたでしょうか？ 今回の問題では平方数が目印として大活躍しています。行数が列数より小さいところ(Ｌ字のタテ線上の整数)は一番上の平方数から戻ればいいでしょう。行数が列数より大きいところ(Ｌ字の横線上の整数)は、Ｌ字終点の平方数からさかのぼるより、始点の数から近づいた方が間違いがなさそうです。始点の数とは一つ前のＬ字の終点に１をたした数ですね。また、場所を特定する問題では、その整数が始点と終点のどちらに近いかを調べることが手がかりになりますね。カドが始点と終点の平均なので、平均より小さい整数ならＬ字の横線上にあり、平均より大きい整数ならＬ字のタテ線上にあります。

算数を長い間教えてきて、生徒が一番よくわかってくれる方法を書きましたけど、僕が書かなかった法則を使うこともできると思います。もし自分の頭になじむうまい法則が見つかったら、ぜひそれもいっしょに活用してください。自慢の法則があったらコメントしてくれてもいいですよ。 楽しみに待ってますね。

それでは今回の講座47はこれで終わります。文章はいくら書いても苦じゃない人なんだけど、図を作るのはプロじゃないから毎回手こずってます。見にくい図だったかな～？(汗) じゃあまた次の講座でお会いしましょうね(*^^)