Newみんなの算数講座20 角材つっこみ問題

みなさんこんにちは。今日も算数しますよ~。
みなさんが読む時間がわからないから、今まではあいさつを書きませんでしたが今回から書くことにしました。礼に始まる算数。いいでしょう?(^^♪
今回の講座では、水の入った容器に角材をつっこんでいくときの水深変化を考えます。角材つっこみ問題とか棒つっこみ問題と言われてますね。お風呂に入ったときを思い出してくれると説明がしやすくなります。
みなさんが水が(お湯ですね)入っているお風呂の湯船に入ると、お湯の水面は上がりますね?湯船が満たされて外にこぼれるかもしれませんが、上がったりこぼれたりしたお湯の体積は、みなさんのカラダのうち、水面より下にあるパーツの体積と等しいです。(パーツ…手とか足とか胴体とか)
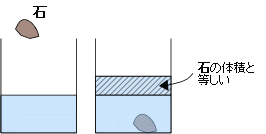
下の絵も同じです。水の入っている容器に石を入れると、石が水面より下に入った分だけ水の深さが上がります。じゃまものと同じ体積だけ水が押しのけられる感じですね。
では問題を出しましょう。
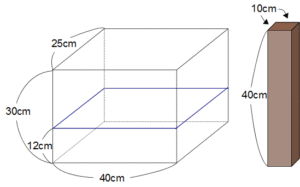
下の図左のようなタテ25cm、横40cm、高さ30cmの直方体の容器があり、12cmの深さまで水が入っています。いま、タテと横10cm、高さ40cmの角材(図右)を底面が容器の底面と平行になるように水の中に入れていきます。
(1)水面が1cm上がるまで角材を入れたとき、角材の底面は容器の底面の何cm上にありますか?
(2)角材の底面が容器の底面につくまで入れたとき、 水の深さは何cmになりますか?
塾で習った人もいますか?初めて見た人は図の書き方をしっかりマスターしてください。こうした問題は、立体を平面におきかえた図を書くことが大事ですよ。いちいち立体の図を書くのは大変ですからね。必ず平面に置きかえましょう。
重要メモ 棒突っ込み問題は立体の図ではなく、正面からみた平面図を書いて考えます。その際、図の横の長さは底面積を記入します。
(1)
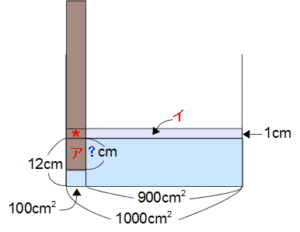
上の図の横線は容器や角材の底面積を表し(長さではありませんよ)タテ線が高さを表しています。すると図の面積が体積を表すことになりますね。
重要メモ 底面積×高さ=体積
容器全体の底面積=25×40=1000cm²
角材の底面積 =10×10=100cm²より、その差は 1000-100=900cm²です。
角材の突入によってアの部分の水が押しつぶされ、イの部分に移動します。湯船にからだをつけたとき、湯面が上昇するのと同じ理屈ですね。つまり、アの部分とイの部分の体積が等しいことになります。
メモ ★の部分にはもともと水がないから、アにもイにも★の部分はふくまれません。
イの部分の体積= 900×1=900cm³
アの部分の高さ(?cm)=900÷100=9cm
したがって容器の底面から角材の底面までの長さは、12-9=3cmです。
(2)
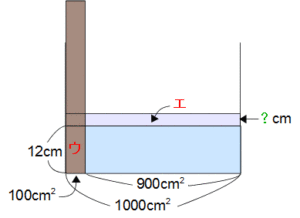
角材の底面が容器の底面につくまで入れると、上の図のようになります。ウの部分の水がエの部分に移動しますね。
ウの部分の体積=100×12=1200cm³
エの部分の高さ(上昇分?cm)=1200÷900=1200/900=4/3cm=1と1/3cm
よって、角材突っ込み後の水の深さは12+1と1/3=13と1/3cmです。
角材つっこみ問題を楽しんでもらえましたか?
じつは今回の問題はまだまだ基本で、もっと複雑な問題もあります。容器に穴があいていたり、突っ込む物体にふたがなくて水が入ったり、突っ込む物体がヘンテコな形をしていたり…。あふれて水がこぼれてしまうパターンもありますよ。しかし基本ができなければ難しい問題はとうてい無理ですから、まずは今回の基本をしっかりおさえてくださいね。
水面下に沈んだ物体の体積の分だけ水面が上昇する
ごくごく自然なことです。図を書いたときに〈最初の水面〉と〈突っ込み後の水面〉を混同しないようしてくださいね。それから突っ込む角材は容器のはじに寄せて書くといいですよ。
では今回の講座はここまでにしましょう。次の講座もどうぞご期待ください!
みなさんへの宿題
講座の問題に続きの設問を作ります。
角材を何本か用意して、角材の底面が容器の底面と平行になるように1本ずつ順に水の中に入れていきます。容器の水があふれてこぼれるのは何本目の角材を入れたときですか。
解答したい方はページ下のコメントに書いてください。正解不正解をレスさせていただきます。お名前はニックネームでもかまいません。














