Newみんなの算数講座12 算数の専売特許0.57倍

今回は、算数では使えるけど数学では使えなくなるという不思議な計算式をお話ししようと思います。
こんな問題がその計算の舞台です。
下の図は、1辺の長さが6cmの正方形の中に2つのおうぎ形を書いたものです。中央にあるレンズ形(さつまいも)の面積は何cm²ですか?円周率は3.14とします。
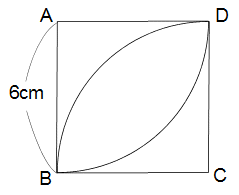
まずは普通に素直に考えてみましょう。下の図のようにレンズ形を2つに分割します。
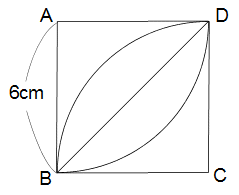
おうぎ形BCDの面積は6×6×3.14×1/4=28.26cm²
メモ おうぎ形の面積=半径×半径×円周率×中心角/360°
三角形BCDの面積は6×6÷2=18cm²
メモ 三角形の面積=底辺×高さ÷2
おうぎ形から三角形を引くとレンズ形の半分の面積になります。
28.26-18=10.26cm² →レンズ形の半分の面積
これを2倍するとレンズ形の面積です。
10.26×2=20.52cm² →レンズ形の面積(答え)
この方法がもっともオーソドックスでしょうね。
ここから冒頭に書いた算数時代だけ使える計算方法の話です。
じつはいまのレンズ形(さつまいも)の面積は、次の式で一発計算できます。
レンズ形の面積=正方形の面積×0.57
中央にあるレンズ形の面積は正方形の面積の0.57倍なのです。確かめてみましょうか。
6×6×0.57=36×0.57=20.52cm²
こりゃ速い!って感じですね。中学受験生が知ってる割合はどれくらいかなあ?半々ぐらいでしょうか。もし知らなかった人は便利なので覚えてくださいね。
 さて、なぜこの計算が算数の専売特許で数学では使えなくなるかというと、それは円周率に理由があります。算数で使う円周率はほとんどの場合3.14です。僕の誕生日は3月14日ですという話は蛇足ですが(笑)、中学以降の数学では3.14という円周率は使わなくなります。
さて、なぜこの計算が算数の専売特許で数学では使えなくなるかというと、それは円周率に理由があります。算数で使う円周率はほとんどの場合3.14です。僕の誕生日は3月14日ですという話は蛇足ですが(笑)、中学以降の数学では3.14という円周率は使わなくなります。
3.14という円周率は3.1415926535 8979323846 2643383279 ………という無限小数を小数第二位までにまるめた近似値(およその数)だから、数学では3.14ではなくパイ(右のイラスト)というギリシャ文字を使うのです。正確ではない近似値を使って求めた答えも正確ではないから、それならパイのままにしておこうというのが数学の立場でしょう。
では円周率を3.14として0.57倍の秘密に迫りますね。
正方形の1辺とおうぎ形の半径を☆とします。さっき6cmだったところが☆ですね。
おうぎ形の面積は☆×☆×3.14×1/4=☆×☆×0.785
三角形の面積は☆×☆÷2 → ☆×☆×0.5
おうぎ形から三角形を引いたレンズ形の半分の面積は
☆×☆×0.785-☆×☆×0.5
=☆×☆×(0.785-0.5)
=☆×☆×0.285 (分配法則で☆×☆を1つにまとめた)
これを2倍するとレンズ形の面積です。
☆×☆×0.285×2=☆×☆×0.57
☆×☆は正方形の面積だから、レンズ形の面積はその0.57倍ということが説明できました。
0.57倍は算数ではとても便利なショートカットですが、円周率3.14が前提にあるので、残念ながら算数時代でおしまいという有効期限付き公式なんですね。でも算数時代は堂々と使えますから、塾のテストや入学試験で大いに活用してほしいと思います。
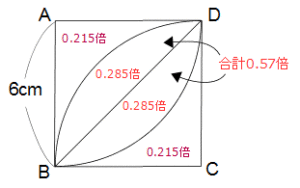
最後に問題の図で、もう少し細かく倍率を示しておきましょう。0.215倍は円の回転移動の問題でよく使いますよ。
(1-0.57)÷2=0.43÷2=0.215倍です。
では今回はこのへんで!また次の講座で一緒に算数を楽しみましょう!
カーテンコール
だいぶ前になりますが、算数指導要領の信じられない改悪で、学校の教科書の円周率が3.14から3に変更されたことがあります。その後わりとすぐに是正されましたが、もし円周率を3にすると、今回の0.57倍は0.5倍になってしまい、レンズ形の面積が正方形の面積のちょうど半分になってしまいます。0.57倍は5割より6割に近いですから、それを半分はアバウトすぎますね。他にも中心角60度のおうぎ形で半径と弧の長さが等しくなってしまったり、円周率3はいろいろ問題を巻き起こしてくれました。この稿を書きながら当時を思い出してしまいました。
みなさんへの宿題
下の図は1辺の長さが10cmの正方形の中に4つの半円を書いたものです。斜線部分の面積は何cm²ですか?円周率は3.14とします。
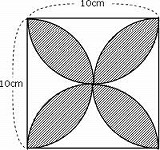
解答したい方はページ下のコメントに書いてください。正解不正解をレスさせていただきます。お名前はニックネームでもかまいません。













