Newみんなの算数講座23 タカヒト君とソウジ君

こんにちは。講座23番ですね。23番はちょっと困った話がありまして、むかし書いた元祖では「みなさんへの挑戦」という回で、問題とヒントだけだったんですね。今回の新改訂ではその趣向はなくす予定なので、何か書かないと欠番になってしまうから、新しい内容を書くことにしました。元祖にはなかった新作ってことになりますね。

新作に選んだのは三角形の話です。三角形といっても単独ではなくて、２コ以上の三角形を比較するときにとても大事な内容です。また得意技でタイトルをこってみましたよ？ タカヒト君とソウジ君の話、楽しみながらご参考ください。

タカヒト君というのは高さの等しい三角形のことなんです。タカさがヒトしい。それを縮めてタカヒト君と名づけてくれたのは以前の教え子の女の子です。すばらしくピッタリなネーミングですよね。

下の図を見てください。

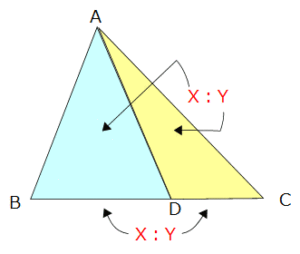
ブルーの三角形ＡＢＤとクリーム色の三角形ＡＤＣは、底辺をＢＤ、ＤＣと見たときに高さが等しいです。高さを示す線は書きませんでしたが、頂点Ａから底辺に対して垂直に引く線が高さです。
底辺のところに赤い字でＸ：Ｙと書きました。アルファベットを使ったのは、どんな数でも大丈夫だから、代表選手としてのアルファベットです。３：２でも４：３でもなんでもＯＫです。

底辺の比がＸ：Ｙで高さは等しいでしょう？ すると面積の比も同じ比のＸ：Ｙになりますよ？ 具体的な面積(□cm²)を求めるときは高さをかけたり、公式の「÷２」をしなくてはなりませんが、面積の比については、等しい高さをかける必要はありません。ン？って人は底辺と高さを好きな数に決めて調べてみるとよいでしょう。せっかく高さをかけても、面積の比は底辺の比に戻ってしまうはずです。

ではタカヒト君の性格(重要事項)まとめます。

次にタカヒト君の親友ソウジ君の話です。
算数や数学を経験した人なら相似という言葉は聞いたことがありますよね？
はい。ソウジ君はまさに相似のことです。

しっかり勉強すれば、タカヒト君とソウジ君の性格の違いはハッキリわかると思いますが、慣れてない生徒はふたりの性格をごちゃごちゃに混同しますね。みなさんはきちんと区別してください。

図をご覧ください。

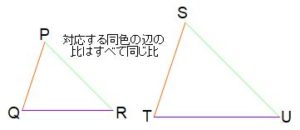
相似というのは、このように同じ形で大きさがちがう図形の関係です。拡大、縮小という言葉のほうが一般的かもしれません。

メモ　小学校の教科書に相似という用語はありません。学校では拡大図、縮図と呼ぶようです。しかし受験の算数ではふつうに相似と呼びますね。相似、覚えてください。

同じ色をつけた辺どうしを対応する辺といいます。相似な図形では、対応する辺の比はすべて同じ比になります。たとえば赤で示したＰＱとＳＴの比がＸ：Ｙだとすれば、緑の辺も紫の辺もＸ：Ｙです。この共通した比のことを相似比と呼びます。また、これは当然に感じるでしょうが、∠Ｐと∠Ｓなど対応する角は同じ角度です。

メモ　∠ → 角を表す数学記号。算数の本には現れませんが、ここでは使いました。

そして相似形の面積の比。

残念ながら相似形の面積の比は相似比と同じではありません。底辺がＸ：Ｙなら高さもＸ：Ｙであり、三角形の面積は底辺と高さをかけるから、相似形の面積の比は相似比を２回かけた(２乗した)比になるのです。ではこのヘンでソウジ君の性格まとめますね。

このように分類して説明すればタカヒト君とソウジ君の性格のちがいをおわかりいただけたと思いますが、現場でよくみかける混乱は、タカヒト君の面積で底辺を２回かけたり、ソウジ君の面積を相似比のままにしたり、などですね。２つの三角形を比較するという点ではよく似てますけど、かなり重要な内容なので混同しないように気をつけてくださいね。最初から当たり前に区別できる人は図形のセンスがなかなかですよ。

では新作なのでもう一個オマケ。タカヒト君でもソウジ君でもない別の個性です。

三角形には〈底辺〉〈高さ〉〈面積〉の３要素がありますね。これらの３要素のうち、２つがわかっていれば３つめの要素の比を作ることができます。もちろん作るときの計算は公式どおりです。タカヒト君のときと同じように、面積の公式の「÷２」のことは気にしないでかまいません。

面積の比＝底辺の比×高さの比
底辺の比＝面積の比÷高さの比
高さの比＝面積の比÷底辺の比

下の図で赤が面積の比、青が底辺の比なら、高さの比は
(５÷２)：(４÷３)＝5/2：4/3＝15/6：8/6＝15：８です。

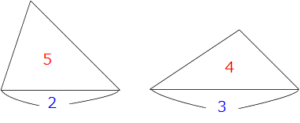
この個性もよく使うので知っておいてください。名前は何にしましょうかね。３つめの比を作るからミツル君とかですか？（笑）

２つの三角形の話。いかがでしたか？このページは逃げたりしませんから、不安に思ったらまたいつでも読み返しにきてくださいね。算数も継続が力なのは言うまでもありません。英語では直訳じゃなくて
Practice makes perfect.
というらしいですよ。練習が完璧を作る？ いい言葉ですね。新作なのでよけいなことまで書いてしまいました。では次の講座でまたお目にかかりましょう。みなさん毎日お元気で！