Newみんなの算数講座21 嵐？TOKIO？EXILE？

今回の講座では、集合といわれるジャンルから、３つの輪が重なるベン図の考え方を解説します。２つの輪は簡単なのですが、３つになると意外な盲点があります。よく読んで知識を増やしてくださいね。

算数や数学で勉強する集合とは、同じ性質をもったいくつかのものの集まりのことです。
たとえば１ケタの偶数の集合は {2、4、6、8}
24の約数の集合は{1、2、3、4、6、8、12、24}です。算数では集合のことを集まりといいますが、この講座では集合と呼ぶことにします。

いくつかの集合の関係を考えるとき、右のようなベン図を用意すると、問題の内容が整理されてわかりやすくなります。２つの輪のベン図については解いたことがある人が多いと思うので、今回は３つの輪のベン図の問題について説明することにします。

では問題を出しますね。
男性アイドルグループランキングを参考にしました

条件が多いですね。これはさすがに頭の中だけでは整理しきれないでしょう？
こんなときこそベン図が役にたちます。さっそく３つの輪のベン図を使って問題を整理してみましょう。

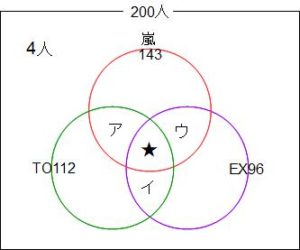
こんなベン図になります。
どのグループも選ばなかった人が４人だから、輪っかの合計は
200－４＝196人です。

嵐を選んだ143人、TOKIOを選んだ112人、EXILEを選んだ96人をすべて加えると、
143＋112＋96＝351人
たし算の結果が輪っかの合計の196人を超えてしまっています。それは重なったところをダブって数えているからです。ダブって数えているところは次のようになっています。

ア…嵐の○とTOKIOの○で２回数えている（１回よぶん）
イ…TOKIOの○とEXILEの○で２回数えている（１回よぶん）
ウ…嵐の○とEXILEの○で２回数えている（１回よぶん）
★…すべての輪で３回数えている（２回よぶん）

つまり、さきほどの合計の351人は、ア、イ、ウを１回ずつと★を２回よぶんに数えているのです。
ダブりをカウントしない人数を求めるために次のような計算をします。

問題の条件から、
ア＋★＝65人
イ＋★＝58人
ウ＋★＝39人
これらをすべて加えて、
（ア＋★）＋（イ＋★）＋（ウ＋★）
＝65＋58＋39＝162人 →ア＋イ＋ウ＋★＋★＋★
この人数をさきほど合計した351人から引くと、ア、イ、ウのダブりについては取りのぞくことができます。
351－162＝189人 →ア、イ、ウのダブりは取りのぞいた

あともう一歩です。この189人は、１回ずつよぶんだったア、イ、ウはうまく消すことができていますが、２回よぶんだった★を３回引いたことで、★の部分は１回引きすぎてしまっています。言葉をかえると、189人は★の部分がカウントされていません。

メモ　少し前の青い線を引いた式を見てください。162人には★が３回ふくまれてます。ダブりを消すためには、★の人数は２回分引けばいいので３回分引いてしまったら1回分引きすぎです。

まもなく着地します。
★を１回分引きすぎた189人に★を1回分をたせば、輪っかの合計の196人になるはずです。
189＋★＝196より、★＝196－189＝７人
これが全部のグループを選んだ人の人数です。

３つの輪が重なるベン図の問題を理解してもらえたでしょうか？

みなさんは輪っかのどの部分に入る人でしたか？(*^^) では今回の講座はこれで終わりますね。次の講座と今回登場してもらったグループの活躍に期待してください！

カーテンコール
Googleアナリティクスという統計ツールによると、むかしのホームページで一番視聴率が高いのは102講座のうち、この講座なのだそうです。他にもいい講座はいっぱいあると思うのですが、これが一番なのはタイトルの人気グループのおかげで検索に出やすいのでしょうね。……というわけでグループ名のタイトルは今回の改訂でもそのままにしました（笑）