Newみんなの算数講座35 最小公倍数までのデータ集め

みなさんこんにちは。今日も僕の算数講座を読みにきてくれてありがとうございます。

講座35と36は元祖の改訂ではなく新しい講座に差し替えることにしました。長い雑談のあとで読者のみなさんに難しい問題を出すという回だったから、 充実した算数講座に整理し直す改訂の趣旨からはずれました(笑) …というわけで35と36は２回連続で未発表の新作を書きますね。

今回の講座35は整数問題のジャンルです。問題の条件にあてはまる数をみつけるために最小公倍数が大活躍しますよ。ではさっそく問題を出しましょう。今回は２問やりますね。まず１問目。

この問題は講座21で扱った集合のベン図を書いて解く方法もあると思います。そっちの方が支持率は高いかもしれないですね。もちろんベン図もいい方法だし、僕もベン図で教えることはありますけど、そうそう、算数は引き出しの数が多い方がなにかと有利ですからね。ここではベン図は押し入れにしまって、最小公倍数までのデータ集めを敢行しようと思います。

３と４の最小公倍数は12ですね？ この12が今回の問題では不動の主役です。次のように１から12までの整数を書き並べてみます。

そしてこの中から問題の条件にふさわしい数を選んでください。ふさわしい数を〇で囲んでもいいし、逆にふさわしくない数を消してもいいです。僕は後者でいきます。３の倍数と４の倍数を消せば、３でも４でも割り切れない整数が残りますね。

このように12個の整数のうち、６個が消えて６個が残ります。
さて、問題で与えられた数の範囲は１から100までですよね？ ここがとても大事なポイントですが、この先の整数を12個ずつまとめて同じ作業をすると、同じ列が消えて同じ列が残っていくのです。ためしにあと一段加えてみますね。

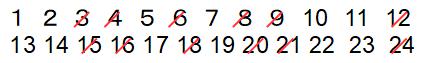
意味おわかりですよね？ ３の下の15は消えていて、５の下の17は残っていて、… のように、消えている数と残っている数はまったく同じ列です。つまり、整数を12個ずつ区切っていくと、問題の条件にふさわしい数が規則正しい位置に６個ずつあることがわかります。(もちろんふさわしくない数も規則的です)

１から100までの範囲には100÷12＝８あまり４より、12個ずつの整数セットは８セットあります。問題にふさわしい数は１セットに６個だから、８セットでは６×８＝48個です。そして「あまり４個」の中にもふさわしい数があることを忘れないでください。セットからはみ出る「あまり４個」は97、98、99、100ですが、これらはセット内の左から４つだから、ふさわしい数が２個ふくまれます。問題の答えは48＋２＝50個です。

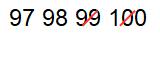
老婆心　12個のうち、半分が消えて半分が残ったのは問題の設定数値による偶然です。最初のセットの調査が一番大事です。最小公倍数までのセット内でふさわしい数の位置と個数をみきわめてください。

題材を分数にして２問目いきましょう。

並んでいる分数が約分できるかできないかは、分子の数と分母の90との関係で決まります。分母の90を素因数分解することが手がかりになりますよ。

90を素因数分解すると２×３×３×５です。ここに現れた２、３、５という素数キャスト(出演者)が大事です。(３の重複は気にしないでかまいません)
分子がこの素数キャストの倍数になっていると約分ができるわけですね。すると分子が２、３、５の倍数でないものが約分できない分数ということになります。その調査にもベン図を使う手がありますが、今回はベン図は押し入れにしまいましたからここでも最小公倍数までのデータを取ることにします。

２、３、５の最小公倍数30までが１セットです。１から30までを書き並べてデータ収集を始めてもよいですが、偶数は２で割れてしまうから、奇数だけを並べて開始しましょう。

このうち３の倍数と５の倍数を消せばよいですね。こうなります。

１から30までの１セットに残っている数は８個です。次のセットは31から60ですが、同じ列が消えて同じ列が残るのは１問目の問題といっしょです。やはり８個の数が残ります。
２セットに続く61から89までの29個の数については、89の次に90を補って同じようなセットで考えてかまいません。90は偶数で消えますからふさわしい数の個数には影響を及ぼしませんからね。つまり61から90までのセット内にもふさわしい数は８個です。２セット目と３セット目の画像は省略しますので、時間があれば書いて調べてみてください。

答えが出ましたよ。約分できない分子は１セットに８個ずつで、そのセットが３セットあるから、全部で８×３＝24個です。

最小公倍数までのデータ集め。なかなか使えそうでしょう？ 与えられた範囲が広ければ広いほどこうした工夫が大事になりますね。この方法がすぐれているのは、規則性をきちんとつかめば範囲がどんなに広がっても対応がきくことです。１問目は押し入れにしまったベン図でも簡単ですが、２問目はベン図だと輪っかが３つになるんですよね。２問目はこっちのデータ集めが優勢かな。きっとみなさんの前にこの考え方が使える問題が現れることがあるでしょう。最小公倍数までのデータ集め。積極的に活用してくださいね。

久々に新作講座を書きましたが楽しんでもらえたでしょうか。楽しみながら頭もよくなってくれたら一番うれしいですよ。次回も新作を発表予定です。なるべく早く出しますからまた読みにきてくださいね。それまでみなさんお元気で！

カーテンコール
じつは今回の問題には一発公式もありまして、(2)の場合は90個×(１－1/2)×(１－1/3)×(１－1/5)＝90×1/2×2/3×4/5＝24個です。90個のうち、1/2が２の倍数ではなく、2/3が３の倍数ではなく、4/5が５の倍数ではないということなんですね。ただしこの公式は90個のところが２、３、５の公倍数に限定されますし、理由を説明するのはやさしくありません。参考にとどめてください。