NEWみんなの算数講座101 正六角形の分割レクチャー

みなさん、こんにちは。前回で大台の100講座に到達しましたから、今回の講座からは、改めて初心にかえった気持ちで書いていこうと思ってます。引き続きの応援をよろしくお願いします。
今回の講座では正六角形の分割について考えてみたいと思います。
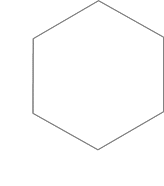 正六角形。右のような図形です。6つの辺の長さ、6つの角の大きさがすべて等しくなっています。六角形の内角の総和は720°だから、1つの内角の大きさは720÷6=120°です。
正六角形。右のような図形です。6つの辺の長さ、6つの角の大きさがすべて等しくなっています。六角形の内角の総和は720°だから、1つの内角の大きさは720÷6=120°です。
*多角形の性質については、31回目の講座をご確認ください。
 本題に入る前に少し雑談を。
本題に入る前に少し雑談を。
正六角形を平面上に並べていくと、右のイラストのように過不足なく平面をうめつくすことができます。きれいですね。難しい言葉ですが、このような性質も持った図形のことを平面充填形(へいめんじゅうてんけい)と言います。それが立体的に発展した場合にはハニカム構造という言葉も使われますよ。蜂(ハチ)の巣の各部屋がハニカム構造になっていることはよく知られています。
ではここから本題です。算数の図形を勉強する上で、知っておくと便利な正六角形の分割をいくつか解説していきます。
その際、正六角形全体の面積を60に決めて解説したいと思います。どんな数に決めても同じなのですが、正六角形の解説では60がうまくいくのです。60という数が2、3、4、5、6のどれでも割り切れる扱いやすい数だからです。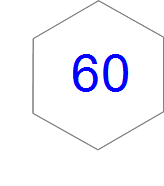
最初は簡単なところから。これはまっぷたつなので30と30で当たり前ですね。
左右どちらの四角形(台形)も全体の1/2(←30/60)です。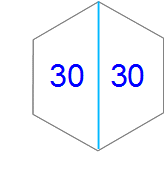
この6等分も難しくないですね。正六角形はこのように3本の対角線によって、6つの合同な正三角形に分割することができます。
どの正三角形も全体からみると1/6(←10/60)です。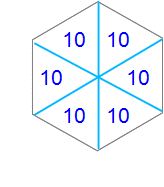
これも6等分なのですが、1つ前とは別の分割です。カドを切り取ったような二等辺三角形が外側に3つ。内側にもそれと合同な二等辺三角形が3つあります。どの二等辺三角形も合同ですから、すべて全体からみると1/6(←10/60)です。
*中央で3つの三角形が交わっている点は、1つ前の図で、3本の対角線が交わっている点と同じ点です。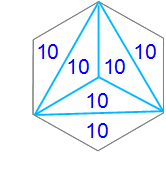
今度は、いままでの分割の図にあった何本かの線を消した分割です。
左側は正六角形の内部に長方形が現れるパターンです。
長方形の面積は全体からみると2/3(←40/60)です。
まん中の図は、その長方形を半分にしたパターンです。中央に2つの直角三角形が現れ、直角三角形の面積は全体からみると1/3(←20/60)です。
右側は、正六角形の内部にさきほどよりひと回り大きな正三角形を残すパターンです。この正三角形の面積は、全体からみると1/2(←30/60)です。さきほどの小さな正三角形の3倍の面積です。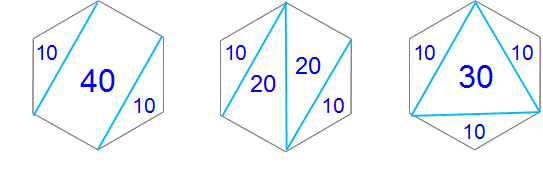
だいたいこのへんまでが基本の分割です。実際に出題される正六角形の分割問題にはもう少しややこしいものもあります。それは分割する線分(上の各図のブルーの線)の片側または両端が、正六角形の頂点ではなく、辺上の別の位置にくる場合です。
ではここで、いつものように例題を出してさらに解説を進めたいと思います。
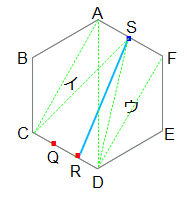
次の各問いに答えてください。青い点は辺のまん中の点、赤い点は辺を3等分した点です。
(1)左の図で、三角形アの面積は正六角形全体の何分のいくつですか?
(2)右の図で、図形イと図形ウの面積の比は何対何ですか?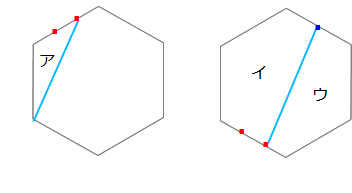
アドバイス
この問題では、正六角形全体の面積を60とすると整数で表せなくなる箇所が出てきます。正六角形全体の面積には180をお勧めします。こうした自由な数のチョイスも算数の面白いところです。もっとも分数計算をいとわないのなら60でも問題ないです。
(1)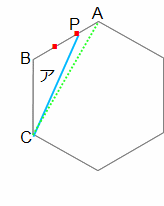 講座の前半で解説したように、△ABCの面積は正六角形の面積の1/6です。正六角形の面積を180とすると、△ABCの面積は180×1/6=30です。
講座の前半で解説したように、△ABCの面積は正六角形の面積の1/6です。正六角形の面積を180とすると、△ABCの面積は180×1/6=30です。
△PBC(ア)と△ABCは高さが等しい三角形だから、面積の比は底辺の比と等しく2:3です。
△PBC(ア)の面積=△ABC×2/3=30×2/3=20
これは正六角形全体からみると20/180=1/9にあたります。
(2) 正六角形の面積を180とします。
正六角形の面積を180とします。
(イの面積)+(ウの面積)=180だから、先にウの面積を考え、イの面積はあとで全体から引き算して求めます。
ウの面積は△FDEと△SDFと△SRDの面積の合計です。順番に考えていきます。
△FDE→正六角形の1/6で30です。…①
△SDF→△ADFの1/2です。〈理由/底辺の比SF:AFが1:2〉
△ADFが正六角形の1/3で60だから、△SDF=60×1/2=30です。…②
△SRD→△SCDの1/3です。〈理由/底辺の比RD:CDが1:3〉
△SCDは△ACDと面積が等しいから〈理由/底辺と高さが等しい〉、△SRDは△ACDと比べても1/3です。△ACDは正六角形の1/3で60だから、△SRD=60×1/3=20です。…③
①、②、③を合計して、(ウの面積)=△FDE+△SDF+△SRD=30+30+20=80
イの面積は、全体の正六角形からウの面積を引いて、180-80=100
よって求める解答(イの面積):(ウの面積)は100:80=5:4です。
***
正六角形の分割レクチャー、いかがでしたか?
ボクが工夫したのは、正六角形の面積を1とせず、前半では60、例題では180とした点です。途中のアドバイスにも書きましたが、こうした数の選び方が算数の自由度です。もちろん教科書どおり全体を1にする手もあると思いますが、全体を1にするといろいろな場所の面積が分数になり、それを分割すれば分数を分割することになり、「面積を表す分数」と「割合を表す分数」が混在し、計算を間違えてしまうケースも増えると思います。できるだけ整数で計算できるとラクですよね。みなさんも正六角形の分割問題では、60や180など、上手な数を使って考えてみてください。
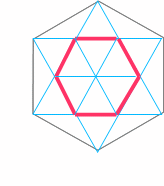 最後に本編で書かなかった分割をオマケします。正六角形は右のようにきれいに18等分することができます。18個の三角形の内訳は、正三角形が12個と二等辺三角形が6個ですが、どの三角形もすべて面積が等しいです。中央に赤で囲んだ正六角形は、18個中6個の三角形で構成されているから、全体の正六角形からみれば6/18=1/3の大きさです。この問題よく見かけます。
最後に本編で書かなかった分割をオマケします。正六角形は右のようにきれいに18等分することができます。18個の三角形の内訳は、正三角形が12個と二等辺三角形が6個ですが、どの三角形もすべて面積が等しいです。中央に赤で囲んだ正六角形は、18個中6個の三角形で構成されているから、全体の正六角形からみれば6/18=1/3の大きさです。この問題よく見かけます。
では今回の講座はこれで終了します。次回は立体の表面積の話をしようと思います。それではまた~。
インフォメーションボード
〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。
〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。
〈算数講座へのご意見や質問/ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。
〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、5講座ずつを1冊子にまとめ、「なかとじ印刷」した片側A5サイズ(開くとA4)のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら











