Newみんなの算数講座41 2倍じゃなくて3倍になる秘密

みなさんこんにちは。どんどん書いてきた算数講座ですが、今回で早くも41講座目になるんですね。いったいこの講座はどこまで続くのでしょう? じつは僕も最初にホームページを立ち上げた頃、こんなに長く続けるつもりはありませんでした。でもたくさんの人のアクセスがうれしくてね。それでここまで延びてきちゃった。もうこうなったら増やし続けるしかないね。僕もがんばるので、みなさんも忘れずに読みにきてくださいね。
*現在全講座の改訂作業中ですが、このあいさつは初めて書いたときのものをそのまま残しました
今回の講座41は二人が2地点間を反対方向から往復する旅人算です。「こんなに出る問題あんまりないよ!」というぐらいよく出題される問題です。どこの塾でも絶対やるから知らないとヤバいかも~。知らない人はしっかり読んでマスターしてください。知っている人にとっては復習のいい機会? 新しい発見もあるかも! お付き合いくださいね。
では問題を出して解説を始めますね。タイトルの意味は読んでいるうちにわかると思います。
A、B2地点間の距離は1200mです。お父さんはA地点を、お母さんはB地点を出発し、ともにAB間の往復を続けます。お父さんの速さは分速90m、お母さんの速さは分速60mです。次の各問いに答えてください。ただし、場所についてはA、Bのうち近い方から離れている距離を答えてください。
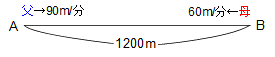
(1)お父さんとお母さんが1回目に出会うのは何分後ですか?また、それはどこですか?
(2)お父さんとお母さんが2回目に出会うのは何分後ですか?また、それはどこですか?
(3)お父さんが前を歩いているお母さんに後方から追いつくのは何分後ですか?また、それはどこですか?
では(1)から。1回目の出会いは簡単だと思います。

離れている二人が同時に向き合って出発すると、二人は合計した速さて近づいてきます。下の公式は超絶大事です。
1200÷(90+60)=8より、二人は8分後に出会うことがわかります。出会う場所は母の速さに8分をかけて、B地点から60×8=480mのところです。
〈重要〉旅人算の出会い公式
離れている距離÷速さの和=出会うまでにかかる時間
次は(2)です。
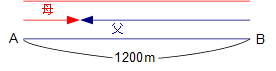
下の図をよく見てください。2回目に出会うときは、父の進んだ距離と母の進んだ距離の合計がAB間の距離の3倍になっていることがわかります。ここが2回目の出会いのポイントなんです。タイトルの意味はこれですよ。
今回のような両方向からの往復問題では、2回目に出会うまでに進む距離の合計は全体の距離の2倍ではなく3倍です。距離が3倍になればかかる時間も3倍になるから、二人が2回目に出会うのは1回目の8分後を3倍して24分後です。
出会う場所は母の速さに24分をかけて60×24=1440m。これは一度A地点で折り返して1440-1200=240mのところです。
続いて(3)です。
父と母がAB間の往復を繰り返しているうちに、どこかで父が母に追いつくという状況が起こります。「追いつく」と「出会う」は意味がちがいますね。(1)と(2)は父と母が反対向きに進んで同じ地点にくるから出会いですが、同じ向きに進んで同じ地点にくれば追いつきです。
父が母に追いつくとは、下の図のように父が母より1200m多く進んだときです。父が母より多く進む距離は1分間に90-60=30mだから、父が母より1200m多く進むのは1200÷30=40分後。追いつく場所は母の速さに40分をかけて60×40=2400m。これは母がちょうど一往復を終えてB地点に戻ったところです。
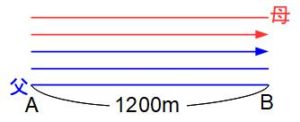
メモ この図は答えを求めてから作った図です。解く前はちょうどB地点で追いつくことはわからないと思いますが、初めて追いつくまでに進んだ距離の差は、追いつく場所に関係なく、最初の隔たりと同じになります。
二人が2地点間を反対方向から往復する旅人算のまとめ
〈1回目の出会い〉二人が進んだ距離の合計=最初の隔たり
〈2回目の出会い〉二人が進んだ距離の合計=最初の隔たりの3倍
〈3回目の出会い〉二人が進んだ距離の合計=最初の隔たりの5倍
〈4回目の出会い〉二人が進んだ距離の合計=最初の隔たりの7倍
*回数が1回増えるごとに、二人が進んだ距離の合計が1倍、3倍、5倍、7倍…と奇数倍に増えていきます。
*所要時間も距離の倍率と同じ倍率で変わります。
注意
出会うだけではなく、速い方が遅い方に追いつくという状況も起こります。
最初の隔たり÷速さの差=速い方が遅い方に追いつくまでの時間
「出会う」と「追いつく」は二人が同じ地点にくることはいっしょですが、算数では区別することがとても多いです。問題をよく読んでください。
お疲れさまでした。今回はちょっとややこしかったかな。じつはあと一点書かなかったことがあるのですが、本文に書くと混乱する人が出そうなのでカーテンコールに書いておきますね。そのことは大きな問題ではないので、基本的には解説した(1)~(3)をしっかり理解してほしいと思います。最初にも書いたようにほんとよく出る問題ですからね。算数を勉強する人には絶対に欠かせない問題ですよ。
では今回の講座はこれでおしまいにしますね。また次の講座で元気にお目にかかりましょう!
カーテンコール
鋭い人は気づいたかもしれませんが、初めの隔たりを5倍して3回目の出会いを求めると、6000÷150=40分後となって初めて追いつくときと一致します。算数では「出会う」「追いつく」という言葉を明確に区別するので、厳密には40分後を3回目の出会いとするのは間違いでしょうね。この点は出題者も気にして作問すると思います。基本的には本文で解説した1回目、2回目の出会いと、初めて追いつくときが求められれば大丈夫です。ちなみに初めの隔たりを7倍すると8400÷150=56分後です。これは出会いで合ってます。40分後は追いつきだから56分後が3回目の出会いということになりますね。興味がある方は正確なダイヤグラムを書いてみるといっそう理解が進むと思います。













