Newみんなの算数講座24 ニュートン算マニュアル

みなさんこんにちは。僕はいま高校野球を見てますが、具体的な内容を書けないのがツラいです。書くと日にちがたつと古くなってしまうでしょう？講座の新鮮さを保ちたいからさ。では今日も算数を楽しく語りますよ(^^♪

今回は苦手な人が多そうなニュートン算を取り上げます。もしかしたら名前も知らないという人がいるかもしれませんね。まずはニュートン算の紹介から～。

ニュートン算とは、初めにある決まった量があり、その量を減らす動きと増やす動きが同時に存在する問題のことです。減らす動きだけなら仕事算といいますが、仕事算とニュートン算のちがいは増える量の存在ですね。ニュートンが最初に出したことからニュートン算という名前がつけられています。ニュートンは物理学者ですが算数もすごく得意だったようですよ。よく出題されるニュートン算には「泉の水をポンプでくみ出す問題」「牛が牧草地の草を食べる問題」「行列を処理する窓口の問題」などがあります。

では基本的なニュートン算からいきましょう。

ニュートン算を式だけで解くのは簡単ではありません。問題文からは直接見えないことがいくつかあるからです。問題の条件を次のような線分図に表すと見えてきますよ。ニュートン算は線分図！忘れないでください。

問題の条件が２つあるから、線分図を上下に並べて書きます。くみ出すのにかかる時間と同じ時間だけわき出る水がありますね。くみ出す水は初めにたまっていた水とわき出る水の合計です。40Ｌずつ16分では640Ｌの水がくみ出され、70Ｌずつ８分では560Ｌの水がくみ出されます。

この線分図が書けたら２本の線の差に注目しましょう。２通りの見方ができてそれらが等しいことがわかります。
・線の差をわき出る水としてみれば 16－８＝８分でわき出る水
・線の差をくみ出す水としてみれば 640－560＝80Ｌ
８分でわき出る水が80Ｌだから１分でわき出る水は80÷８＝10Ｌです。
では初めの泉の水は？
16分でわき出る水が10×16＝160Ｌだから、これを640Ｌから引いて、初めの泉の水は640－160＝480Ｌです。

さて問題で聞かれているのは５分で空にするときの１分間にくみ出す量です。初めの泉の水480Ｌを４分で空にするためには１分で480÷４＝120Ｌの水を減らす必要がありますが、１分にわき出る10Ｌもうめなくてはならないから、１分間に120＋10＝130Ｌの水をくみ出せばよいことがわかります。

解説では使わずに済ませてしまいましたが、次の仕上げ公式は覚えておくとよいでしょう。問題の条件をあてはめて確認することができますし、わからない箇所がひとつなら逆算することもできます。

ではもう一問。いまの問題より少し難しいと思います。

最初の問題とのちがいは、減らす量や増える量が具体的に書かれていないことです。もちろんそこがわからなくても答えは出せるのですが、ちょっとした工夫をほどこす必要がありますよ。線分図を書いてみます。

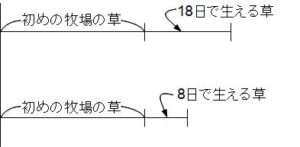
ここまでは難しくないですね。問題は牛が食べた草をどのように表現するか？ です。
ここで１頭の牛が１日で食べる草の量を１という比で考えることにします。１頭×１日＝１のように牛の頭数と日数をかけ算する要領です。この比の量はオレンジ色で表示しますね。みなさんが解くときは①のように〇で囲んで比を表すとよいと思います。
線分図は次のようになります。

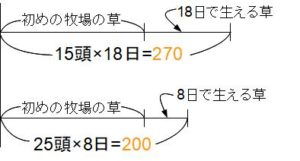
２本の線の差に注目するのはさきほどと同じです。
・線の差を生える水としてみれば 18－８＝10日で生える草
・線の差を牛が食べる草としてみれば 270－200＝70
10日で生える草が70だから１日で生える草は70÷10＝７です。
下の線を使って初めの牧場の草を計算します。８日で生える草が７×８＝56だから、これを200から引いて、初めの牧場の草は200－56＝144です。

(1)求めるのは牛が31頭のときの草がなくなる日数です。仕上げ公式を使いましょう。
初めの牧場の草÷(１日に牛が食べる草－１日に生える草)＝草がなくなる日数 ですね。
144÷(31×１－７)＝144÷(31－７)＝144÷24＝６日間で草はなくなります。
＊31頭の牛が１日で食べる草は31×１＝31ですが、初めから31と書いても同じです。

(2)求めるのは４日で草がなくなるときの牛の頭数です。仕上げ公式を使って逆算しましょう。
144÷(□×１－７)＝４日　この式を逆算して□＝43頭です。

以上、ニュートン算の解説でした。減らす量や増える量が明示されている問題は難しくないですね。やはりそこが明示されてない２問目が大変ですかね。最大のポイントは１頭×１日＝１のように減らす量を比で表現するところでしょう。たしかに〈単位のある２つの量をかけて無単位の量を作る〉という点は他の文章題ではあまりみないテクニックですね。しかしそこをニュートン算の特長としてクリアーしてもらえれば、ニュートン算が得意分野にできると思います。ニュートン算が苦手な人は、どこかで難しく考えすぎて迷路に迷い込んでしまうことが多いようです。今回の講座を参考に、しっかり線分図を書いて落ちついて解くようにしてくださいね。

今回は長くなりました。最後まで読んでくれてありがとうね。ではまた次の講座でお会いしましょう。それまでお元気で！

カーテンコール
途中にも少し書きましたが、ニュートン算をx、yなどの文字を使って解くのは苦労がたえません。２問目の問題などは３つの文字が必要になりますし、しかもその文字がいくつになるかは最後までわからない不定方程式という普通とはちがう方程式になってしまいます。数学より算数がすぐれていることは少なくないですね(*^^)