Newみんなの算数講座62 見えないものが見える人に

みなさんこんにちは。ここはニューみん算講座62です。
 今回は立体図形に水を入れる問題ですが、タイトル候補がふたつあって、「見えないものが見える人に」を選びましたが「王様の発想」というタイトルも捨てがたくて迷いました。見えない洋服が見えるとウソをつき、町じゅうをはだかでパレードしたはだかの王様の話は有名ですよね。今回の講座はあの話のイメージを持ちながら読んでもらうとよいでしょう。では問題を出しますね。
今回は立体図形に水を入れる問題ですが、タイトル候補がふたつあって、「見えないものが見える人に」を選びましたが「王様の発想」というタイトルも捨てがたくて迷いました。見えない洋服が見えるとウソをつき、町じゅうをはだかでパレードしたはだかの王様の話は有名ですよね。今回の講座はあの話のイメージを持ちながら読んでもらうとよいでしょう。では問題を出しますね。
下の左図のような容器に4.5cmの深さまで水が入っています。容器は密閉されていて外に水はこぼれません。容器を下の右図のようにタテに置きなおしたとき、水の深さは何cmになりますか? 図中の数値の単位はcmです。
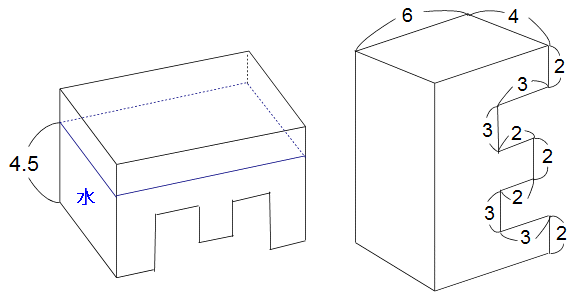
アルファベットEのレタリング立体ですね。なぜEかというと、この問題を出題した学校の頭文字がEだからです。六本木にある東洋英和ですね(^^)/
さてみなさんならどうやって解きますか? まず水の体積を求める? う~ん、それでもできそうですけど、水の体積を出すのはちょっと大変ですよね~。
もっといい方法があります!最初に振っておいた話ですよ。 この問題ははだかの王様の考えで解くと早いのです。
つまりね、左の容器に入っている水を見るのではなく、水を見るのはふつうの民衆
水の上に入っている目に見えない空気を見るのです。これが王様の発想!
水の方はギザギザな形だから体積を出すのが面倒だけど、空気の方なら単純な直方体でしょう? どう考えても水の体積より空気の体積を出す方が簡単ですよね。ではさっそく空気の体積を計算してみます。
空気のタテの長さ…4cm
空気の横の長さ…2+3+2+3+2=12cm
空気の高さ…6-4.5=1.5cm
空気の体積…4×12×1.5=72cm³
さて、左の状態から右の状態に容器を置きなおしても、水や空気の体積が変わることはないから、右側の立てた状態でも、水の上に 72cm³の空気があるはずです。
では右側の立てた立体を上から5段に分けて考え、必要なところまで体積を計算してみます。
立てた状態で1番上の段の体積…6×4×2=48cm³
空気の体積は 72cm³だから、1番上の段だけでは空気が入りきりません。
立てた状態で上から2段目の体積…3×4×3=36cm³
一番上の段の体積をたすと48+36=84cm³
これは72cm³より多いから、2段目までをすべて空気にすると空気が多すぎてしまいます。つまり、空気は上から2段目の途中まで入っていることがわかります。
上から2段目に必要な空気の体積は 72-48=24cm³です。
その空気の高さは〈高さ〉=〈体積〉÷〈底面積〉より、24÷(3×4)=24÷12=2cm
この計算から、2段目は上から2cmまでが空気になり、2段目に入る水の高さが3-2=1cmとわかります。この1cmに上から3段目、4段目、一番下の段の高さを加えて、立体を立てたときの水の深さは1+2+3+2=8cmと求めることができます。
王様の発想、いかがでしたでしょうか? 容器内の空気は本当に人の目には見えないから、見えない洋服が見えると言った王様と同じウソにはなりませんが、見えない方を見てほしいという意味で、僕は今回のような考え方を王様の発想と呼んでいます。普通誰しも、容器に水が入っていればその水を見てしまいたくなるものです。それをあえて見ずに、見にくい逆を見ることで問題が簡単に解ける場合があるという例でした。難しいことは何もなく、ちょっとした発想の切り替えなんですけどね。意外と盲点になる人もいるのではないかと思い、今回の講座を書きました。王様の発想、頭のどこかに残しておいてくださいね。
では今回の講座62はこれで終わりです。宿題も書きましたから考えてみてください。正解不正解が気になるときはコメントを入れてくれたらお返事しますからね。
次回は久々に食塩水です。面積図やてんびんが使えない問題なども扱いたいと思います。どうぞお楽しみに~!
みなさんへの宿題
下の図のように、1辺の長さが8cmの立方体を4個組み合わせた形の容器に、上の段の2.4cmの高さまで水が入っています。この容器にふたをして密閉し、赤い線で囲んだ面が床につくように置き直すと、水の深さは何cmになりますか?
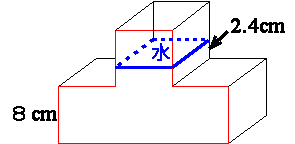
解答したい方はページ下のコメントに書いてください。正解不正解をレスさせていただきます。お名前はニックネームでもかまいません。













