Newみんなの算数講座16 加比の理で解く図形問題

今回の講座では「同じ比どうしをたしても同じ比」という加比の理(かひのり)の考え方を使って図形の問題にせまります。理解してもらえたら図形問題のレベルアップは間違いないでしょう。
問題を出す前に、加比の理について簡単な例で説明しておきます。
さくらさんが2000円、桃子さんが1500円持っていたとします。2人の所持金の比は? 簡単ですね。4:3です。
この2人がやさしいイサオおじさんからおこづかいをもらいました。さくらさんが400円、桃子さんが300円です。もらったおこづかいの比は? はい。これも4:3です。
では、初めの所持金にもらったおこづかいを加えてみましょう。さくらさんは 2400円、桃子さんは 1800円 になります。おこづかいをもらったあとの2人の所持金の比は? そうそう、これもまた4:3なのです。
この例のように、ある決まった比(A:B)の量に対して、同じくA:Bの量を加えたとき、合計の量もA:Bとなり、このような性質を算数では加比の理と呼んでいます。当たり前だと感じた人は比に対するセンスが備わっていましたね。(たすのではなく引いても同じことです)
さて、このことを使って解く図形の問題があります。わりとよく見かけますよ。しっかり読んでしっかり理解してくださいね。
下の図形において、EG:GCを求めてください。
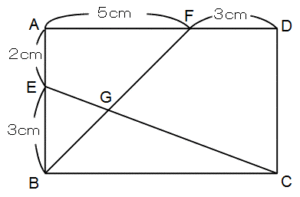
解説の前にこの問題で使う図形の基本を1つ確認しておきます。
高さが等しい三角形の面積の比は、底辺の比と等しい
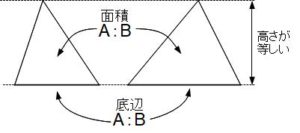
では問題の解説です。
求めるのはEG:GCですが、この長さを直接求めるのではなく、面積の比がEG:GCと等しくなる三角形を探します。EG:GCと等しくなる三角形の面積の比を答えれば、それはEG:GCを答えたことと同じですよね?
△EBGと△GBCの底辺をEG、GCとみると、2つの三角形の高さは等しいから、EG:GCは△EBGと△GBCの面積の比と同じです。しかし残念ながら△EBGと△GBCの面積を求めるのは簡単ではありません。
補助線EF、FCを引いてみましょう。
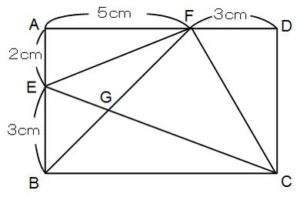
面積の比がEG:GCの比と等しくなる三角形がまた1組現れました。△FEGと△FGCです。しかしこれらの面積も簡単には求めることができません。
ここで加比の理の登場です。
△EBGと△GBCの面積の比=EG:GC
△FEGと△FGCの面積の比=EG:GC でしたよね?
するとこれらをタテにたした面積の和もEG:GCの比になるはずです。これぞまさに加比の理!
△EBGと△FEGをたせば△EBFになり、△GBCと△FGCをたせば△FBCになります。
△EBFと△FBCの面積なら三角形の面積の公式で簡単に求められますね。
△EBF=3×5÷2=7.5cm²
△FBC=8×5÷2=20cm²
これで答えがわかりました。EG:GCの長さの比は、△EBFと△FBCの面積の比と等しいから7.5:20
これを整数の比に直して3:8が解答となります。
メモ 比は両側に同じ数をかけても割ってもかまわないから、7.5:20はまず2倍して15:40 これを5で割って3:8です
加比の理で解く図形の問題、理解してもらえたでしょうか?
面積の比がEG:GCの比になる三角形が3組あって、その中で簡単に面積を求められるのが加比の理を使って合計した△EBFと△FBCという仕掛けでした。
今回の問題は相似形を利用するなど他の解き方もあります。図形の問題は解き方がひとつということはほとんどなくて、いろいろな解き方があるのが普通です。引き出しの数が多い人ほど有利ということですね。加比の理の解き方はメジャーではありませんが、なかなかユニークな解き方ではないかと思います。使えることもけっこうあると思うので、頭の引き出しにしまっておいてくださいね。
では今回の講座はこれで終わります。また次の講座で元気にお会いしましょう。風邪とか引かないでくださいね。
みなさんへの宿題
下の図で、BG:GFの比を求めてください。
解答したい方はページ下のコメントに書いてください。正解不正解をレスさせていただきます。お名前はニックネームでもかまいません。
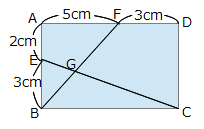
-
前の記事

Newみんなの算数講座15 積み木くずし
-
次の記事

Newみんなの算数講座17 生徒に教わった年令算











