NEWみんなの算数講座88 移項がないからさ

ニューみん算講座。90講座に向けてまた一歩前進します。末広がりの八十八回目は、マイナスの数を使わない算数の個性について書こうと思います。

算数の問題を解くとき、なんとか式は作れたけど、そこからの処理に困って正解を逃がすというパターンがあると思います。それはおそらく単純な四則計算ではなくて、□を求めるような逆算で、□が「＝」の両側に分かれていたり、□に何かがかけ算されていたり、「＋☆」や「－★」といった尻尾(しっぽ)がついていたり？
数学では方程式を習うから、中学生以上の人ならそうした式も処理できるはずですが、悲しいかな算数では方程式が使えません。「算数でも方程式を使えばいいのに」という意見もありそうですが、０より小さいマイナスの数が定義（用意）されていない算数では、方程式を使うことには無理があるのです。

数学では、０はド真ん中の数 です。０の片側が１、２、３、４、５、……という算数でも使う 「プラスの数」で、０の反対側には－１、－２、－３、－４、－５、……という「マイナスの数」 があります。しかし算数では「マイナスの数」は世の中にないものとしてやっています。

算数がマイナスの数を使わない理由は、具体的に存在する（目に見える）数の範囲で問題を考えることが算数という科目の大前提だからです。「何もない状態を０」と考えるのは良いとして、「何もない０より小さい」というのは具体的ではない難しい話でしょう？数学ではそれをマイナスの数を用意して考えるわけですが、それはあくまで「何もない０より小さい数がある」と定義しているだけなんですよね。算数はその抽象的な話には付き合わないということです。

今回は前置きが長くなってしまいました。そろそろ問題を出さないといけないですね。では算数の問題を解くとき、方程式っぽい式を乗り切るにはどうしたらよいか？次の４問を題材にしましょう。

(1)と(2)は□を未知数にしました。

どちらも「＝」の両側に□がありますね。
「移項して整理すれば簡単じゃないの？」
９×□－３×□＝32－８　ですか？
上にも書きましたが、算数にはマイナスの数がないから、「＝」を越えると符号が逆になる移項は苦しいです。「－」を「マイナス」ではなく「引く」と読ませて逆算で説明をすることは無理ではないですが、教える方も習う方も大変です。

ではどう乗り越えるか？
こんな方法がよいと思います。

(1)
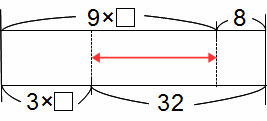
下のような線分図で表します。
矢印のところに注目すると、
６×□＝24　➡　□＝24÷６＝４　です。
＊□９個分と□３個の差は□６個分。32と８の差は24。

線分図を書かない簡略法もありますが、それは最後に説明します。

(2)
今度は、無理して移項しようとしてもマイナスがたくさん出てくる数字設定です。
12×□－６＝15×□－24
12×□－15×□＝－24＋６
これを　－３×□＝－18　➡　□＝(－18)÷(－３)＝６
とやらせるのでは教わっている小学生は大混乱です。
最初の式の両辺を入れかえて、
15×□－24＝12×□－６　としておけば、いくらかマシですが、
15×□－12×□＝－６＋24となりますから、右辺の式は算数にない式です。
やはり線分図がわかりやすいです。矢印の部分で３×□＝18がわかれば、

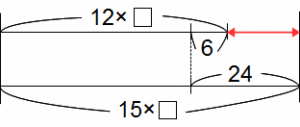
□＝18÷３＝６と簡単に□を求めることができます。

(3)
今度は□ではなく①を求めます。最初にも書きましたが、算数では□と①は同じ意味です。線分図はこのような感じになりますね。

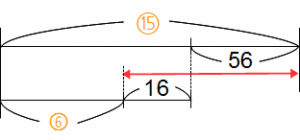
もう解説は不要でしょうかね。
矢印の部分から⑨＝72。したがって①＝72÷９＝８が正解です。

(4)
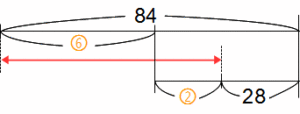
最後の問題です。⑥と②を近づけたかったので、下の線を右側から書くという工夫をしましたが、問題の式の84－⑥＝②＋28　が表現できています。
この線分図さえ書ければ簡単です。
矢印に注目して⑧＝56。したがって①＝56÷８＝７が正解です。

＊＊＊
ここまではよいですか？どの問題も、式を線分図で表すことで、「＝」の両側に分かれている未知数を求めることができました。

さて、途中に書いたように、実際は線分図を書かなくても解答することが可能です。時間の短縮にもなりますから、次の方法も頭に入れておいてください。

では例題から２問選んでやってみます。

(1)
９×□＋８＝３×□＋32
「＝」の左側…９も３も式の先頭で「＋★」扱い　➡　差でまとめて６×□
「＝」の右側…＋８と＋32　➡　差でまとめて24
６×□＝24
□＝４

(4)
84－⑥＝②＋28
「＝」の左側…－⑥と、式の先頭で＋扱いの②　➡　和でまとめて⑧
「＝」の右側…式の先頭で＋扱いの84と＋28　➡　差でまとめて56
⑧＝56
①＝７

方程式がない算数では、このような工夫で「＝」の両側に未知数が分かれている式を計算します。面倒と思う方もいると思いますが、このような工夫こそ算数の個性のひとつです。もし方程式を勉強することで文章題がスラスラ解けるなら、算数でも方程式を教えるべきかもしれませんが、おそらくそれほどの効果はないでしょう。方程式を使うことで、算数らしい柔軟な発想が奪われることが多いからです。つまり算数において、方程式が使えないことで不自由になることは、ごく限られた場合と言えるでしょう。

最後にもう一点。
式を作ったときに、３×(７×□＋12)＝５×(10×□－16)　のようになった場合は、分配法則を使って(　　)をはずす必要があります。
「３×」や「５×」を(　　)の中の両方にかければ（　　）ははずれます。
３×７×□＋３×12＝５×10×□－５×16 ですね。
かけ算できるところをかけ算して、
21×□＋36＝50×□－80
もう大丈夫ですね。□はみなさんが求めてください。

では今回は少し長くなりましたが、これでおしまいにします。また次回の講座を楽しみにお待ちください。

カーテンコール
実際の文章題で、今回解説した内容がピタッとはまる問題をあげておきましょう。
「現在両親の年令の和は90才、三人の子どもの年令の和は16才です。両親の年令の和が三人の子どもの年令の和の３倍になるのは何年後ですか？」
□年後または①年後として式を立ててお考えください。
90＋２×□＝(16＋３×□)×３　または　90＋②＝(16＋③)×３
かっこをはずして
90＋２×□＝48＋９×□　または　90＋②＝48＋⑨
解答は６年後です。

インフォメーションボード

〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。

〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。

〈算数講座へのご意見や質問／ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。

〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、５講座ずつを１冊子にまとめ、「なかとじ印刷」した片側Ａ５サイズ（開くとＡ４）のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら