NEWみんなの算数講座81 数え方のアタリマエ

こんにちは。前回節目の80回目を迎えまして、今回からは100講座が目標です。もちろん100回で終わらせるつもりはないですが、受験生といっしょで目標は励みになりますからね。

というわけで今回は81回目。「数え方のアタリマエ」と題して、４年生以上の人なら理解できるやさしい内容を書こうと思います。むかし書いた11回目の講座にも関連しますが、大事なことなのでもう一度書くことにしました。ではさっそく問題から。

１、３、５、７、９の数字が書かれたカードが１枚ずつあります。このなかから３枚のカードを選んで並べてできる３ケタの３の倍数は何通りありますか？

これは場合の数というジャンルの問題ですね。
うまくいく例を書くと、１、３、５のカードを使えば、どのように並べても３の倍数が作れます。
１３５÷３＝４５
３１５÷３＝１０５
５１３÷３＝１７１
どれも３で割り切れるから３の倍数ですね。

そうそう、知っている人も多いと思いますが、３の倍数には次のような特徴があります。

３の倍数の性質

各位の数字の合計が３の倍数のとき、その整数は３の倍数である！

例　１３５
１＋３＋５＝９　➡　９は３の倍数　➡１３５は３の倍数

このように各位の数字をすべてたしたとき、その合計が３の倍数になる整数は必ず３の倍数ですから覚えておいてくださいね。

＊いろいろな倍数の判定法について６回目の講座にまとめてありますから、ぜひ参考にしてください。

話を戻します。
１、３、５の数字を並べて３ケタの整数を作ると、並べ方は全部で６通りあります。さっきもその一部を書きましたが、今度は全部書いてみましょう。

１３５、１５３、３１５、３５１、５１３、５３１

６通りありますね。次のポイントも知っておくとよいでしょう。

【順列】Ｐ個の違うものを並べる場合の数
　＝Ｐから始めて、１までの整数をすべてかけ算した積（通り）

（例）上の問題では３つの違う数字を並べるから　３×２×１＝６（通り）

＊同じものがあるときは、この計算ではダメなので気をつけてください。
たとえば３枚のカードが１、３、５ではなく１、１、３の場合は、６通りではなく、
１１３、１３１、３１１の３通りです。

ここまでの話は準備です。ここから問題の解答を考えていきましょう。

今回のような問題では、上に書いたような同じカードの並び替え（１３５、１５３のような）のことはあと回しにして、
まず最初に、５枚のカードうち、どの３枚を選べば３の倍数が作れるかという選び方のパターンを先に考えます。
（１、３、５）以外に（３、５、７）のように選んでもＯＫです。３＋５+７＝15（３の倍数）だから、３、５、７を選んでも３の倍数が作れますね。

じつはこのような３の倍数が作れる３枚のカードを選び方は全部で４パターンあるのですが、どうすればその４パターンをモレなく探すことができるでしょう？じつはこの作業がとても大事なポイントなのです。ところが、この作業をしっかりできる人が意外に少ないです。行き当たりばったりの雑な調べ方など、そのときはたまたま合っていても、不安定なやり方をする人が多いです。

今回は僕がていないなやり方を示しておきますから、みなさんが問題を解くときの参考にくださいね。

〈３の倍数が作れる３枚のカードの選び方を調べるお手本〉
・小さい順に調べます。一番小さいのは135、次が137ですね。
（１、３、５）（１、３、７）（１、３、９）（１、５、７）（１、５、９）……

このとき、右に現れる数字が左の数字より小さくなるものは考えません。
（１、５、３）はふくまれていないでしょう？
それは（１、５、３）は（１、３、５）と数字の並ぶ順番がちがうだけだから、ここでそれをふくめると、あとあとおかしなことになってしまうのです。
左の数字＜右の数字　を守ってください。
＊数字が並ぶ順番のちがうものは、解説の最後でちゃんと計算します。

では10通りのカードの選び方と、それらの数字の合計、並べたときに３の倍数が作れるかどうかを書いておきます。異なる５枚のカードから３枚を選ぶパターンは全部で10通りです。この問題ではそのことも知っていると有利です。（組み合わせ　14回目の講座参照）

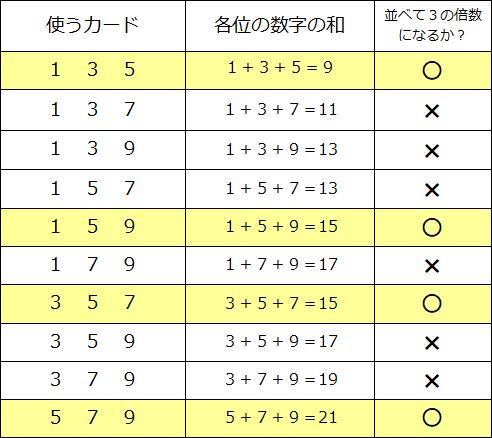
この表のなかで、並べたときに３の倍数ができるカードの選び方は、黄色い色をつけた４パターンです。

問題の解答は４通りではないですよ？　最後に大切なことを考えて解答に着地です。
いま上の表であげた４パターンは数字の組み合わせを選んだだけなので、それぞれに並び替えがあることを忘れてはいけません。並び替えがそれぞれ６通りあることは最初にも少しふれました。
１、３、５の並べ替えは、
１３５、１５３、３１５、３５１、５１３、５３１でしたね。

このことは表の４パターンすべてに同じだから、問題の解答は、
４×６＝24通り　です。

＊＊＊
数え方のアタリマエ、どうでしたか？わかりやすかったかな？　表まで作らなくてもよいですが、10通りを書いてていねいに調べるのが基本方針です。思いついた順番に広い上げるのはダメなやり方で、モレが生じやすいです。たかだか10通りです。こうした問題に慣れてくると判断も早くなりますし、それほど時間もかからなくなるでしょうね。
じつはこの問題にはさらにおもしろい広がりがあります。使用する数字に０が入っていたり、あるいは同じ数字のカードが何枚かふくまれていたり。そんな広がりについてはそのうちまた書きたいと思います。
ではみなさん次回の講座までお元気で！

NEWみんなの算数講座への質問やご意見、筆者ウタマル先生へのお便りは、メールのイラストをクリックして、メールフォームからお寄せください。